Câu hỏi:

11/07/2024 15,285

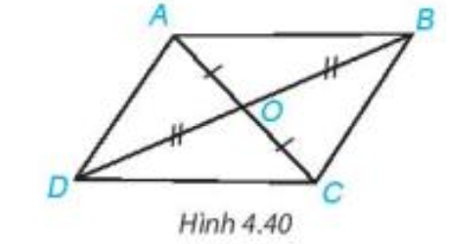
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

b) Chứng minh rằng $Δ D A B = Δ B C D .$

Xem lời giải

Câu hỏi trong đề: Bài tập Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Xét hai tam giác AOD và COB có:

OA = OC (theo giả thiết).

$\hat{A O D} = \hat{C O B}$ (2 góc đối đỉnh).

OD = OB (theo giả thiết).

Vậy $Δ A O D = Δ C O B$ (c – g – c).

Xét hai tam giác AOB và COD có:

OA = OC (theo giả thiết).

$\hat{A O B} = \hat{C O D}$ (2 góc đối đỉnh).

OB = OD (theo giả thiết).

Vậy $Δ A O B = Δ C O D$ (c – g – c).

b) Do $Δ A O D = Δ C O B$ nên AD = BC (2 cạnh tương ứng).

Do $Δ A O B = Δ C O D$ nên AB = CD (2 cạnh tương ứng).

Xét hai tam giác DAB và BCD có:

AD = BC (chứng minh trên).

AB = CD (chứng minh trên).

BD chung.

Vậy $Δ D A B = Δ B C D$ (c – c – c).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho Hình 4.32, biết $\hat{O A B} = \hat{O D C},$ OA = OD và AB = CD. Chứng minh rằng:

a) AC = DB;

b) $Δ O A C = Δ O DB.$

Xem đáp án

Lời giải

a) Do AB = CD nên AB + BC = CD + BC.

hay AC = DB.

Vậy AC = DB.

b) Xét hai tam giác OAC và ODB có:

OA = OD (theo giả thiết).

$\hat{O A C} = \hat{O D B}$ (theo giả thiết).

AC = BD (chứng minh trên).

Vậy $Δ O A C = Δ O D B$ (c – g – c).

Câu 2

Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?

Xem đáp án

Lời giải

Xét tam giác MNP có $\hat{M} + \hat{N} + \hat{P} = 180 ° .$

Do đó $\hat{M} = 180 ° - \hat{N} - \hat{P} = 180 ° - 50 ° - 70 ° = 60 ° .$

Xét hai tam giác ABC và MNP có:

AB = MN (theo giả thiết).

$\hat{B A C} = \hat{N M P}$ (cùng bằng 60^o).

AC = MP (theo giả thiết).

Vậy $Δ A B C = Δ M N P$ (c – g – c).

Câu 3

Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Vẽ $\hat{x A y} = 60 ° .$ Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm,

AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27). Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40. a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau. b) Chứng minh rằng ΔDAB=ΔBCD.

Bình luận

Cho Hình 4.32, biết OAB^=ODC^, OA = OD và AB = CD. Chứng minh rằng: a) AC = DB; b) ΔOAC=ΔODB.

Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?

Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.

Vẽ xAy^=60°. Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27). Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

b) Chứng minh rằng $Δ D A B = Δ B C D .$

Cho Hình 4.32, biết $\hat{O A B} = \hat{O D C},$ OA = OD và AB = CD. Chứng minh rằng:

a) AC = DB;

b) $Δ O A C = Δ O DB.$

Vẽ $\hat{x A y} = 60 ° .$ Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm,

AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27). Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.