Câu hỏi:
07/01/2020 22,314Từ các chữ số thuộc tập X = {0;1;2;3;4;5;6;7} có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
Giả sử số lập được có dạng 
Ta có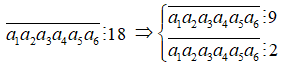 
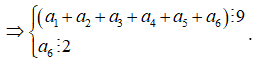
Vì 
nên ta có các trường hợp sau
Trường hợp 1: được chọn từ 
+ Có 3 cách chọn chọn
+ Có 5! cách chọn chọn bộ 5 số 
Suy ra có 3.5! = 360 số.
Trường hợp 2: được chọn từ 
+ = 0, có 5! cách chọn bộ 5 số 
+ 0 khi đó có 3 cách chọn, có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3: được chọn từ 
+ = 0, có 5! cách chọn bộ 5 số
+ 0 khi đó có 1 cách chọn, có 4 cách chọn và có 4! cách chọn bộ 4 số
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8
Đã bán 211
₫ 119.000
₫ 45.000
Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025
Đã bán 104
₫ 136.000
₫ 38.000
Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack
Đã bán 1k
₫ 104.000
₫ 52.000
Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack
Đã bán 218
₫ 130.000
₫ 75.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một hộp đựng 20 viên bi khác nhau được đánh số từ 1 đến 20. Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại. Hỏi có bao nhiêu cách lấy để kết quả thu được là một số chia hết cho 3?
Xem đáp án »
07/01/2020
46,337
Câu 2:
Trong mặt phẳng cho 10 điểm phân biệt. Số vectơ khác , có điểm đầu và điểm cuối lấy trong các điểm đã cho là
Xem đáp án »
07/01/2020
29,317
Câu 3:
Số cách chọn ra 3 học sinh trong số 10 học sinh không tính thứ tự là
Xem đáp án »
07/01/2020
22,072
Câu 4:
Cho k, n (k < n) là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
Xem đáp án »
07/01/2020
17,755
Câu 5:
Trong mặt phẳng cho 18 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác có các đỉnh thuộc 18 điểm đã cho là
Xem đáp án »
07/01/2020
13,706
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)
-
23 câu Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luậnNguyễn Ngọc Thiện
21:33 - 01/04/2024
Câu hỏi
Cho tập hợp A={ 0; 1; 2; 3; 4; 5; 6; 7} . Từ tập A có thể lập được bao nhiêu số tự nhiên có 6 chữ số khác nhau đôi một sao cho các số này là số lẻ và chữ số đứng ở vị trí thứ 3 luôn chia hết cho 2. Giải giúp với ạ