Cho tứ diện ABCD có có tam giác vuông tại B. Biết . Quay tam giác ABC và AB (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:
Cho tứ diện ABCD có có tam giác vuông tại B. Biết . Quay tam giác ABC và AB (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:
Quảng cáo
Trả lời:
Đáp án B
|
Khối nón N1 được sinh bởi tam giác ABC khi quay quanh AB có chiều cao h1=AB và bán kính đáy R1=BC . Khối nón N2 được sinh bởi khi quay quanh AB có chiều cao h2=AB và bán kính đáy R2=AD. Do hai khối nón cùng có chiều cao AB nên hai đáy của hai khối nón nằm trong hai mặt phẳng song song. |
|
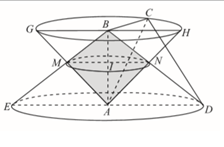
Trong mặt phẳng đáy của hình nón (N1) kẻ đường kính GH//DE. Dễ dàng chứng minh được DEGH là hình thang cân.
Gọi
Khi đó phần chung giữa hai khối nón (N1) và (N2) là hai khối nón:
Khối nón (N3) đỉnh B, đường cao BI, bán kính đáy
Khối nón (N4) đỉnh A, đường cao AI, bán kính đáy
Thể tích phần chung
Áp dụng định lí Ta-let ta có:
Dễ thấy I là trung điểm của
Vậy
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
|
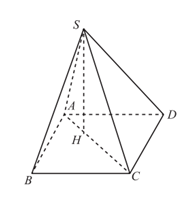
Gọi H là hình chiếu của S trên AC. Ta có Ta có: Ta có: Xét vuông tại S ta có: |
|
Áp dụng hệ thức lượng cho vuông tại S và có đường cao SH ta có:
Lời giải
Đáp án C
Gọi điểm thỏa mãn
Ta có:
Ta có
Do đó nhỏ nhất khi và chỉ khi MI nhỏ nhất là hình chiếu của I trên (P)
Ta thấy
Nên hình chiếu của I trên (P) là chính nó
Do đó
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.