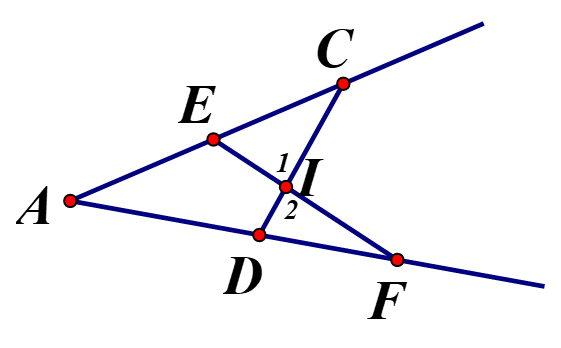
Bước 3 của giải phương trình chứa ân ở mẫu là :
B.Giải phương trình nhận được sau khi khử mẫu
C. Quy đồng mẫu hai vế của phương trình rồi khử mẫu
D. Đối chiếu điều kiện và chọn nghiệm
Câu hỏi trong đề: Bài tập theo Tuần toán 8- Tuần 26 !!
Quảng cáo
Trả lời:
Đáp án B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
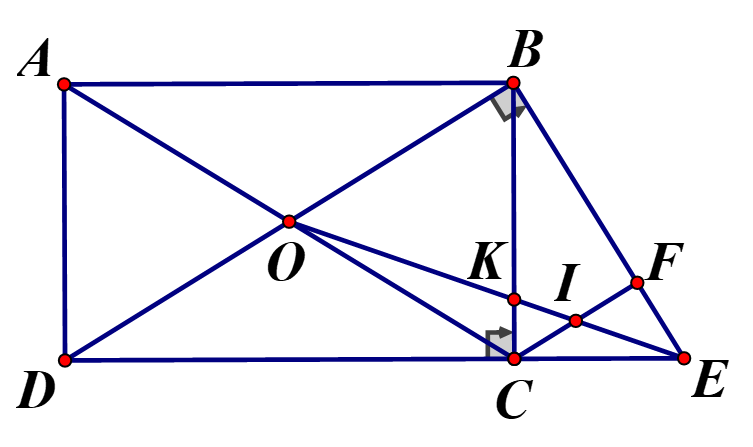
a) Xét và có:
b) Vì là hình chữ nhật nên
Áp dụng hệ thức lượng trong có:
c) Vì
Ta có: có
có
Từ (1) và (2) suy ra
Mà
Vậy I là trung điểm CF
d) Xét và có:
(hệ quả Ta let)
Vậy thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. Có thể vô nghiệm, có thể có một nghiệm duy nhất, cũng có thể vô số nghiệm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.