13 Bài tập tính suất điện động cảm ứng (có lời giải)
62 người thi tuần này 4.6 788 lượt thi 13 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 3 đề thi cuối kì 2 Vật lí 12 Cánh diều cấu trúc mới có đáp án - Đề 3
Bộ 3 đề thi cuối kì 2 Vật lí 12 Cánh diều cấu trúc mới có đáp án - Đề 2
Bộ 3 đề thi cuối kì 2 Vật lí 12 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 3 đề thi cuối kì 2 Vật lí 12 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 3
Bộ 3 đề thi cuối kì 2 Vật lí 12 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 2
Bộ 3 đề thi cuối kì 2 Vật lí 12 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
Bộ 3 đề thi giữa kì 2 Vật lí 12 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 3
Bộ 3 đề thi giữa kì 2 Vật lí 12 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
Từ thông qua một vòng dây của cuộn dây là: \(\Phi = {\rm{BS}}\cos \alpha \), trong đó \(\alpha = 0\) và \({\rm{S}} = \pi {{\rm{r}}^2}.\) Xét trong khoảng thời gian từ \({{\rm{t}}_0} = 0\) đến thời điểm t, từ thông qua 1 vòng dây thay đổi từ \({\Phi _0}\) đến \({\Phi _t}\) ứng với cảm ứng từ là \({{\rm{B}}_0} = {10^{ - 2}}\;{\rm{T}}\) và \({{\rm{B}}_{\rm{t}}} = 0.\)
Theo định luật Faraday ta có suất điện động qua N vòng dây của cuộn dây là:
\({\rm{e}} = - {\rm{N}}\frac{{\Delta \Phi }}{{\Delta {\rm{t}}}} = - {\rm{NS}}\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}\)
Cường độ dòng điện xuất hiện trong cuộn dây là: \(i = \frac{e}{R}\)
Trong đó, \({\rm{R}} = {\rm{L}}{{\rm{R}}_0} = {\rm{N}}2\pi {\rm{r}}{{\rm{R}}_0}\) là điện trở của khung dây.
Do đó, \({\rm{i}} = - {\rm{N}}\pi {{\rm{r}}^2}\frac{{\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}}}{{{\rm{N}}2\pi {\rm{r}}{{\rm{R}}_0}}} = - \frac{{\rm{r}}}{{2{{\rm{R}}_0}}} \cdot \frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}} = - \frac{{0,1}}{{2 \cdot 0,5}} \cdot \frac{{0 - {{10}^{ - 2}}}}{{{{10}^{ - 2}}}} = 0,1\;{\rm{A}}.\)
Lời giải
Hướng dẫn giải:
Ta có 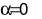 và
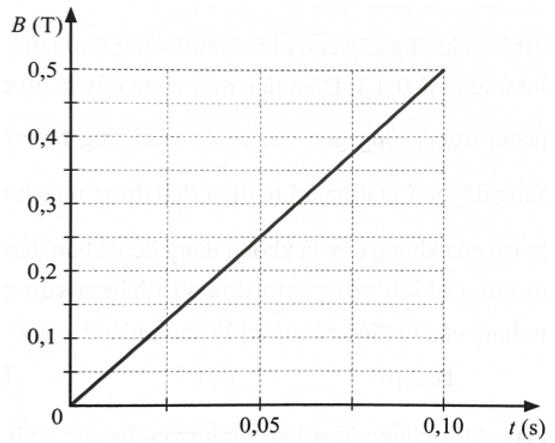
và  , nên \(|{\rm{e}}| = \left| { - {\rm{N}}\frac{{\Delta \Phi }}{{\Delta {\rm{t}}}}} \right| = \left| { - {\rm{S}}\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}} \right| = \left| { - 0,{1^2} \cdot \frac{{0,5}}{{0,05}}} \right| = 0,1V.\)
, nên \(|{\rm{e}}| = \left| { - {\rm{N}}\frac{{\Delta \Phi }}{{\Delta {\rm{t}}}}} \right| = \left| { - {\rm{S}}\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}} \right| = \left| { - 0,{1^2} \cdot \frac{{0,5}}{{0,05}}} \right| = 0,1V.\)
Lời giải
Hướng dẫn giải:
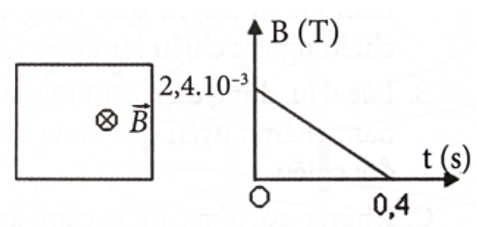
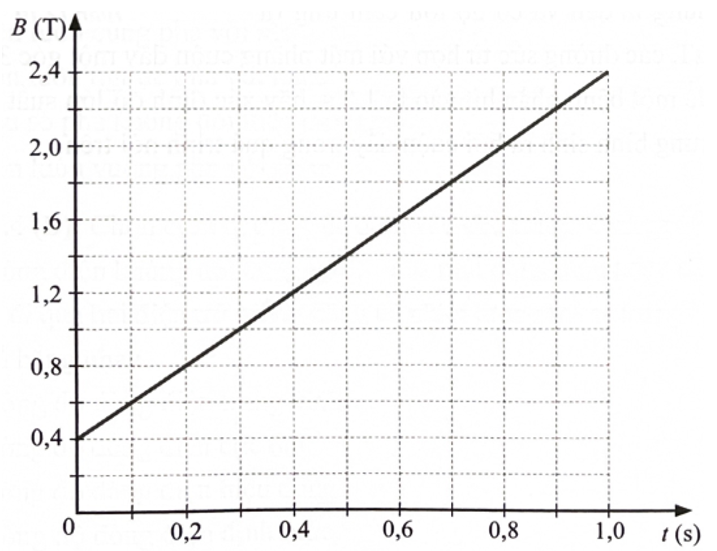
a) Tại thời điểm \({t_0} = 0\) thì \({B_0} = 2,4 \cdot {10^{ - 3}}\;{\rm{T}}\); thời điểm \({\rm{t}} = 0,4\;{\rm{s}}\) thì \({{\rm{B}}_{\rm{t}}} = 0\;{\rm{T}}\) và góc \(\alpha = 0.\)
Do đó, ta có \(\Delta \Phi = {\Phi _{\rm{t}}} - {\Phi _0} = {\rm{NS}}.\Delta {\rm{B}} = 10 \cdot 25 \cdot {10^{ - 4}} \cdot \left( {0 - 2,4 \cdot {{10}^{ - 3}}} \right) = - {6.10^{ - 5}}\;{\rm{Wb}}.\)
b) Theo định luật Faraday ta có: \({\rm{e}} = \left| { - \frac{{\Delta \Phi }}{{\Delta {\rm{t}}}}} \right| = \frac{{6 \cdot {{10}^{ - 5}}}}{{0,4}} = 1,5 \cdot {10^{ - 4}}\;{\rm{V}} = 0,15{\rm{mV}}.\)
c) Cảm ứng từ B giảm nên theo định luật Lenz cảm ứng từ do dòng điện cảm ứng sinh ra sẽ cùng chiều với cảm ứng từ B. Theo quy tắc bàn tay phải, tìm được chiều dòng điện cảm ứng theo chiều kim đồng hồ chạy trong cuộn dây.
Lời giải
Hướng dẫn giải:
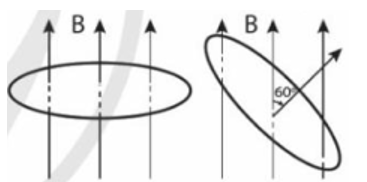
a) \[\left| {{e_c}} \right| = N\left| {\frac{{BS\cos \alpha }}{{\Delta t}}} \right| = 1.\left| {\frac{{0,{{2.30.10}^{ - 4}}.\cos 60^\circ }}{{0,5}}} \right| = {6.10^{ - 4}}V\]
b) Dòng điện có hướng ngược chiều kim đồng hồ (nhìn từ trên xuống vòng dây).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 2,5 V.
B. -5 V.
C. -2,5 V.
D. 5 V.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 225 mW.
B. 22,5 mW.
C. 0,09 mW.
D. 9 W.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
 vuông góc với mặt phẳng khung. Trong khoảng thời gian t = 0,05 s, cho độ lớn của
vuông góc với mặt phẳng khung. Trong khoảng thời gian t = 0,05 s, cho độ lớn của