Thi Online Trắc nghiệm Phép tính lũy thừa với số mũ tự nhiên có đáp án ( Vận dụng )
Trắc nghiệm Phép tính lũy thừa với số mũ tự nhiên có đáp án ( Vận dụng )
-
1074 lượt thi
-
5 câu hỏi
-
30 phút
Câu 1:
Tìm số tự nhiên n thỏa mãn 25n: 253= 255?
Ta có: 25n: 253= 255
Vì 25n: 253= 25n – 3
Nên ta được: 25n – 3= 255
Do đó: n – 3 = 5
Suy ra: n = 5 + 3 = 8
Vậy n = 8.
Chọn đáp án D.
Câu 3:
Tìm số tự nhiên m thỏa mãn 202018< 20m< 202020?
Ta có: 202018< 20m< 202020
Suy ra: 2 018 < m < 2 020
Mà m là số tự nhiên nên m = 2 019.
Vậy m = 2 019.
Chọn đáp án B.
Câu 4:
Không tính các lũy thừa, hãy so sánh A và B với A = 2711và B = 818.
Ta có: A = 2711= (3 . 3 . 3)11 = (33)11=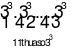 
= 
= 33 . 11= 333
Lại có: B = 818= (3 . 3 . 3 . 3)8= (34)8=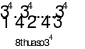 
= 
= 34 . 8= 332
Vì 33 >32 nên 333>332hay 2711>818
Vậy A >B.
Chọn đáp án B.
Câu 5:
Chữ số tận cùng của số 475là:
Ta có: 47 . 47 = 47 . (40 + 7) = 47 . 40 + 47 . 7
= 47 . 40 + (40 + 7) . 7
= 47 . 40 + 40 . 7 + 7 . 7
Suy ra 47 . 47 có chữ số tận cùng như chữ số tận cùng của 7 . 7 = 49.
Do đó 472có chữ số tận cùng là 9
Tương tự (472)2có chữ số tận cùng của 92= 81.
Mà (472)2= 472. 472= 47 . 47 . 47 . 47 = 474
Do đó 474có chữ số tận cùng là 1.
Vậy 475= 474. 47 có chữ số tận cùng là 1 . 7 = 7.
Chọn đáp án A.
Các bài thi hot trong chương:
( 1.4 K lượt thi )
( 1.2 K lượt thi )
( 3.1 K lượt thi )
( 1.6 K lượt thi )
( 1.6 K lượt thi )
( 1.5 K lượt thi )
( 1.5 K lượt thi )
Đánh giá trung bình
0%
0%
0%
0%
0%