Cho hình vẽ dưới đây:
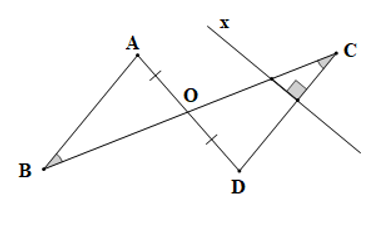
Xét các khẳng định:
(1) BA = CD;
(2) x BA.
Chọn câu đúng:
Cho hình vẽ dưới đây:
Xét các khẳng định:
(1) BA = CD;
(2) x BA.
Chọn câu đúng:
A. Chỉ có (1) đúng;
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Ta có: mà hai góc này ở vị trí so le trong nên AB // CD (dấu hiệu nhận biết)
Do đó (hai góc so le trong)
Xét ABO và DCO có:
(chứng minh trên),
AO = OD (giả thiết),
(hai góc đối đỉnh)
Do đó ABO = DCO (g.c.g)
Suy ra AB = CD (hai cạnh tương ứng)
Khi đó (1) đúng.
Ta lại có AB // CD (chứng minh trên) mà x CD (giả thiết)
Do đó x AB. Nên (2) đúng.
Vậy cả (1) và (2) đều đúng, ta chọn phương án C.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Xét OIM và OIN có:
(do Oz là tia phân giác của ),
OI là cạnh chung,
Do đó OMI = ONI (cạnh huyền – góc nhọn)
Suy ra IM = IN (hai cạnh tương ứng)
Mà IM = 2 cm (giả thiết)
Nên IN = 2 cm
Vậy độ dài đoạn thẳng IN là 2 cm.
Lời giải
Đáp án đúng là: C
• Vì AD // BC nên , (hai góc so le trong).
Do đó C là sai.
• Vì DB // AC nên (hai góc so le trong).
Do đó D là đúng.
• Xét ABD và BAC có:
(chứng minh trên),
AB là cạnh chung,
(chứng minh trên)
Do đó ABD = BAC (g.c.g).
Do đó A là đúng.
• Vì ABD = BAC (chứng minh trên)
Suy ra AD = BC (hai cạnh tương ứng)
Xét AOD và BOC có:
(vì ),
AD = BC (chứng minh trên),
(vì )
Do đó DAOD = DBOC (g.c.g).
Do đó B là đúng.
Vậy ta chọn phương án C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. AIB = MIN;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Cho ABC và MNP có Để ABC = MNP theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
Cho ABC và MNP có Để ABC = MNP theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
A. AB = MN;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Chỉ (I) đúng;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập