Một mảnh đất hình chữ nhật có chu vi là 28 mét, độ dài đường chéo bằng 10 mét. Tính chiều dài và chiều rộng của mảnh đất đó theo mét.

(Đề thi vào 10 TP Hà Nội năm học 2018-2019)

Gọi x, y (m) lần lượt là chiều dài và chiều rộng của khu vườn hình chữ nhật. Điều kiện: \[x > y > 4.\]

Chu vi của khu vườn là 280 m, nên ta có:

\[2\left( {x + y} \right) = 280 \Leftrightarrow x + y = 140.\] (1)

Sau khi làm lối đi thì chiều dài và chiều rộng của hình chữ nhật là \[x - 4;{\rm{ }}y - 4.\]

Diện tích đất để trồng trọt là: \[\left( {x - 4} \right)\left( {y - 4} \right) = 4256.\] (2)

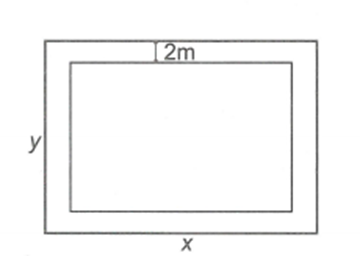
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 140\\\left( {x - 4} \right)\left( {y - 4} \right) = 4256\end{array} \right.\)

Từ (1) ta có: \[y = 140 - x,\] thay vào (2) ta được:

\[\left( {x - 4} \right)\left( {136 - x} \right) = 4256 \Leftrightarrow {x^2} - 140x + 4800 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 60\\x = 80\end{array} \right.\]

Nếu \[x = 80\] thì \[y = 60\] (thỏa mãn).

Nếu \[x = 60\] thì \[y = 80\] (loại).

Vậy khu vườn có chiều dài 80m và chiều rộng 60m

• Giải chi tiết

Gọi x (m) là độ dài một cạnh góc vuông. Điều kiện: \[0 < x < 10.\]

Độ dài cạnh góc vuông còn lại \[x + 2\] (m).

Theo đề bài ta có phương trình:

\[{x^2} + {\left( {x + 2} \right)^2} = {10^2} \Leftrightarrow 2{x^2} + 4x - 96 = 0 \Leftrightarrow \]

Vậy độ dài các cạnh góc vuông là 6m và 8m.