Chứng minh định lí: “Nếu một tứ giác \[ABCD\] có tổng các cạnh đối bằng nhau \[AB + CD = BC + AD\] thì tứ giác đó ngoại tiếp được một đường tròn” bằng cách chứng minh các tia phân giác của bốn góc \[A,B,C,D\] cùng gặp nhau tại một điểm.
Chứng minh định lí: “Nếu một tứ giác \[ABCD\] có tổng các cạnh đối bằng nhau \[AB + CD = BC + AD\] thì tứ giác đó ngoại tiếp được một đường tròn” bằng cách chứng minh các tia phân giác của bốn góc \[A,B,C,D\] cùng gặp nhau tại một điểm.
Quảng cáo
Trả lời:
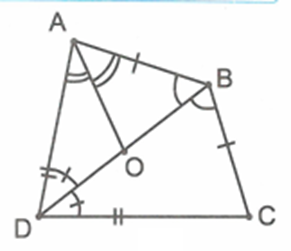
Ta chỉ cần chứng minh các tia phân giác của ba góc \[A,B,D\] gặp nhau tại một điểm. Xét hai trường hợp:
Trường hợp 1: Nếu \[AB = BC\] thì từ giả thiết suy ra \[CD = AD\].
Xét \[\Delta ABD\] và \[\Delta CBD\] có \[AB = BC\], \[AD = DC\] và \[BD\] chung nên \[\Delta ABD = \Delta CBD\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right)\].
Do đó \[BD\] là đường phân giác của các góc \[B\] và \[D\].
Gọi \[O\] là giao điểm của tia phân giác góc \[A\] với \[BD\]. Suy ra \[BO,DO\] là các tia phân giác của các góc \[B\] và \[D\].
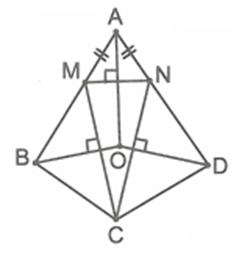
Trường hợp 2: Nếu \[AB \ne BC\], giả sử \[AB > BC\], suy ra \[DA > DC\].
Lấy điểm \[M\] trên \[AB\], điểm \[N\] trên \[AD\] sao cho \[BM = BC,DN = DC\].
Từ giả thiết suy ra \[AM = AN\]. Các đường phân giác của các góc \[A,B,D\] chính là các đường trung trực của tam giác \[CMN\] nên chúng gặp nhau tại một điểm \[O\].
Vậy điểm \[O\] là tâm của đường tròn nội tiếp tứ giác \[ABCD\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Làm tương tự ví dụ 3, ta tính được: \[r = 4\sqrt 5 {\rm{ cm}}\] (với \[r\] là bán kính đường tròn nội tiếp hình thang \[ABCD\]), \[AB = 6\sqrt 5 {\rm{ cm}},CD = 12\sqrt 5 {\rm{ cm}}\].
Do đó diện tích hình thang \[ABCD\] là:
\[{S_{ABCD}} = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {6\sqrt 5 + 12\sqrt 5 } \right).8\sqrt 5 }}{2} = 360{\rm{ c}}{{\rm{m}}^{\rm{2}}}\]
Lời giải
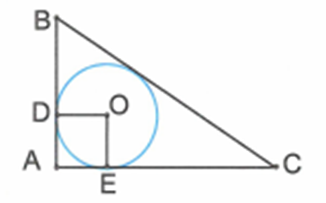
Áp dụng định lí Pitago trong tam giác vuông \[ABC\], ta tính được \[BC = 5{\rm{ cm}}\].
Theo ví dụ 2, ta có: \[AD = AE = \frac{{AB + AC - BC}}{2} = \frac{{3 + 4 - 5}}{2} = 1{\rm{ cm}}\].
Mà \[ADOE\] là hình vuông nên \[r = OD = OE = AD = AE = 1{\rm{ cm}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.