Cho x, y là hai số thực thỏa x>yxy=1.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2x−y

Với x>y,xy=1 ta có: P=x2+y2x−y=x−y2+2xyx−y=x−y+2x−y≥Cosi2x−y2x−y=1(Do..x>y⇒x−y>0) Dấu “=” xảy ra ⇔x−y=2x−y⇔x−y2=2⇔x−y=2⇒x=y+2 Mà xy=1⇔y+2y=1⇔y2+2y=1⇔y2+2y−1=0⇔y=6−22(tm)y=−6−22( Khi đó x=1y=26−2=6+22 Vậy giá tri nhỏ nhất của P là 22 tại x=6+22;y=6−22

Câu hỏi:

13/07/2024 1,538

Cho x, y là hai số thực thỏa $\{\begin{cases} x > y \\ x y = 1 \end{cases} .$ Tìm giá trị nhỏ nhất của biểu thức $P = \frac{x^{2} + y^{2}}{x - y}$

Xem lời giải

Câu hỏi trong đề: Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Với $x > y, x y = 1$ ta có:

$P = \frac{x^{2} + y^{2}}{x - y} = \frac{{(x - y)}^{2} + 2 x y}{x - y} = (x - y) + \frac{2}{x - y} \overset{C o s i}{\geq} 2 \sqrt{(x - y) \frac{2}{x - y}} = 1 (D o .. x > y \Rightarrow x - y > 0)$ Dấu “=” xảy ra $\Leftrightarrow x - y = \frac{2}{x - y} \Leftrightarrow {(x - y)}^{2} = 2 \Leftrightarrow x - y = \sqrt{2} \Rightarrow x = y + \sqrt{2}$

Mà $x y = 1 \Leftrightarrow (y + \sqrt{2}) y = 1 \Leftrightarrow y^{2} + \sqrt{2} y = 1 \Leftrightarrow y^{2} + \sqrt{2 y} - 1 = 0 \Leftrightarrow [\begin{array}{l} y = \frac{\sqrt{6} - \sqrt{2}}{2} (t m) \\ y = \frac{- \sqrt{6} - \sqrt{2}}{2} \end{array} ($

Khi đó $x = \frac{1}{y} = \frac{2}{\sqrt{6} - \sqrt{2}} = \frac{\sqrt{6} + \sqrt{2}}{2}$

Vậy giá tri nhỏ nhất của P là $2 \sqrt{2}$ tại $x = \frac{\sqrt{6} + \sqrt{2}}{2}; y = \frac{\sqrt{6} - \sqrt{2}}{2}$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho (O;R) và một đường thẳng (d) không cắt (O). Dựng đường thẳng $O H ⊥ d$ tại điểm H. Trên đường thẳng d lấy điểm K (K khác H), qua K vẽ hai tiếp tuyến $K A, K B$ với (O), (A, B là tiếp điểm) sao cho $A, H$ nằm về hai phía của đường thẳng OK

Chứng minh tứ giác KAOH nội tiếp

Xem đáp án

Lời giải

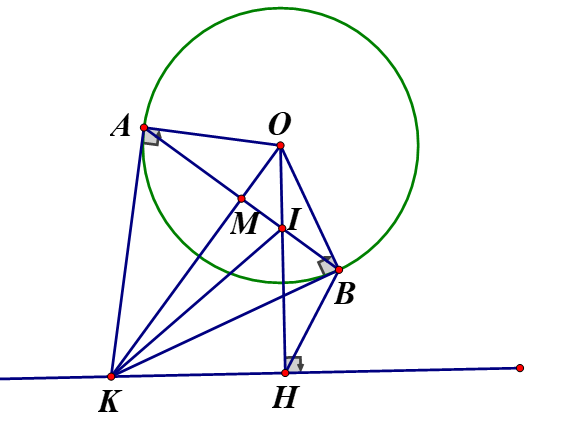
Cho (O;R) và một đường thẳng (d) không cắt (O). Dựng đường thẳng OH vuông góc d tại điểm H. (ảnh 1)

Vì KA là tiếp tuyến của (O) nên $A K ⊥ O A \Rightarrow \hat{K A O} = 90^{0}$

Lại có : $\hat{O H K} = 90^{0} ($ do $O H ⊥ d)$

Xét tứ giác AOKH có $\hat{O A K} + \hat{O H K} = 90^{0} + 90^{0} = 180^{0}$ mà 2 góc ở vị trí đối nhau nên OAKH là tứ giác nội tiếp (dhnb)

Câu 2

1. Cho phương trình : $x^{2} - (m - 1) x - m = 0.$ Tìm m để phương trình có một nghiệm bằng 2. Tính nghiệm còn lại

Xem đáp án

Lời giải

Thay nghiệm x= 2 vào phương trình ta được:

$2^{2} - (m - 1) .2 - m = 0 \Leftrightarrow 4 - 2 m + 2 - m = 0 \Leftrightarrow 3 m = 6 \Leftrightarrow m = 2$

Thay m= 2 vào phương trình ta được: $x^{2} - x - 2 = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array}$

Vậy với m=2 phương trình đã cho có 1 nghiệm bằng 2, nghiệm còn lại x=-1

Câu 3

b, Đường thẳng AB cắt đường thẳng OH tại I. CMR: $I A . I B = I H . I O$ và I là điểm cố định khi điểm K chạy trên đường thẳng d cố định

Khi $O K = 2 R, O H = R \sqrt{3} .$ Tính diện tích $Δ K A I$ theo R

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

c, Khi $O K = 2 R, O H = R \sqrt{3} .$ Tính diện tích $Δ K A I$ theo R

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

b,Rút gọn biểu thức A khi $1 \leq x \leq 2$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Giải phương trình $3 (x - 1) = 5 x + 2$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho x, y là hai số thực thỏa x>yxy=1.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2x−y

1. Cho phương trình : x2−m−1x−m=0. Tìm m để phương trình có một nghiệm bằng 2. Tính nghiệm còn lại

b, Đường thẳng AB cắt đường thẳng OH tại I. CMR: IA.IB=IH.IO và I là điểm cố định khi điểm K chạy trên đường thẳng d cố định Khi OK=2R,OH=R3. Tính diện tích ΔKAI theo R

c, Khi OK=2R,OH=R3. Tính diện tích ΔKAI theo R

b,Rút gọn biểu thức A khi 1≤x≤2

Giải phương trình 3x−1=5x+2

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho x, y là hai số thực thỏa $\{\begin{cases} x > y \\ x y = 1 \end{cases} .$ Tìm giá trị nhỏ nhất của biểu thức $P = \frac{x^{2} + y^{2}}{x - y}$

1. Cho phương trình : $x^{2} - (m - 1) x - m = 0.$ Tìm m để phương trình có một nghiệm bằng 2. Tính nghiệm còn lại

b, Đường thẳng AB cắt đường thẳng OH tại I. CMR: $I A . I B = I H . I O$ và I là điểm cố định khi điểm K chạy trên đường thẳng d cố định

Khi $O K = 2 R, O H = R \sqrt{3} .$ Tính diện tích $Δ K A I$ theo R

c, Khi $O K = 2 R, O H = R \sqrt{3} .$ Tính diện tích $Δ K A I$ theo R

b,Rút gọn biểu thức A khi $1 \leq x \leq 2$

Giải phương trình $3 (x - 1) = 5 x + 2$