- Muốn chia đơn thức A cho đơn thức B (B ≠ 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến đó trong B, ta làm như sau:
+ Chia hệ số của đơn thức A cho ............;
+ Chia lũy thừa của biến trong A cho .............;
+ Nhân các kết quả vừa tìm được với nhau.
Tức là axm : bxn = ............... ( a ≠ 0; b ≠ 0; m, n ∈ ℕ; m ≥ n).
- Muốn chia đa thức P cho đơn thức Q ( Q ≠ 0 ) khi số mũ ở biến của mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi ........... của đa thức P cho đơn thức Q rồi .........các thương với nhau.
Tức là ( A + B ) : C = A : ... + B : C ; ( A – B ) : C = A : ... – ... : C.
- Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:
Bước 1
+ Chia đơn thức bậc ........... của đa thức ........cho đơn thức ........... của đa thức...........;
+ ........kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng ...........;
+ Lấy đa thức bị chia ........... tích đặt dưới để được đa thức mới.
Bước 2. Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc ......... bậc của đa thức chia.
- Muốn chia đơn thức A cho đơn thức B (B ≠ 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến đó trong B, ta làm như sau:
+ Chia hệ số của đơn thức A cho ............;
+ Chia lũy thừa của biến trong A cho .............;
+ Nhân các kết quả vừa tìm được với nhau.
Tức là axm : bxn = ............... ( a ≠ 0; b ≠ 0; m, n ∈ ℕ; m ≥ n).
- Muốn chia đa thức P cho đơn thức Q ( Q ≠ 0 ) khi số mũ ở biến của mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi ........... của đa thức P cho đơn thức Q rồi .........các thương với nhau.
Tức là ( A + B ) : C = A : ... + B : C ; ( A – B ) : C = A : ... – ... : C.
- Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:
Bước 1
+ Chia đơn thức bậc ........... của đa thức ........cho đơn thức ........... của đa thức...........;
+ ........kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng ...........;
+ Lấy đa thức bị chia ........... tích đặt dưới để được đa thức mới.
Bước 2. Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc ......... bậc của đa thức chia.
Quảng cáo
Trả lời:
- Muốn chia đơn thức A cho đơn thức B (B ≠ 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến đó trong B, ta làm như sau:
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B;
+ Chia lũy thừa của biến trong A cho lũy thừa của biến đó trong B;
+ Nhân các kết quả vừa tìm được với nhau.
Tức là axm : bxn = \[\frac{a}{b}\].( xm : xn ) = \[\frac{a}{b}\]xm – n ( a ≠ 0; b ≠ 0; m, n ∈ ℕ; m ≥ n).
- Muốn chia đa thức P cho đơn thức Q ( Q ≠ 0 ) khi số mũ ở biến của mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của đa thức P cho đơn thức Q rồi cộng các thương với nhau.
Tức là ( A + B ) : C = A : C + B : C ; ( A – B ) : C = A : C – B : C.
- Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:
Bước 1
+ Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia;
+ Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột;
+ Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2. Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
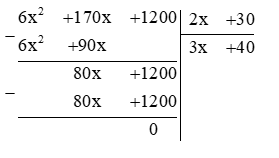
Lời giải
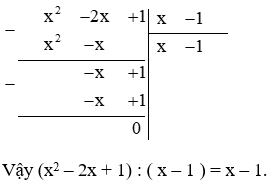
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.