Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là
Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là
A. AE;
B. DC;
C. ED;
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D

Ta có ∆ABC cân tại A (giả thiết) suy ra (tính chất)
BD là tia phân giác góc B nên
CE là tia phân giác góc C nên
Do đó
Xét ∆BEC và ∆CDB có:
BC là cạnh chung
(chứng minh trên)
Suy ra ∆BEC = ∆CDB (g.c.g)
Do đó BE = CD (hai cạnh tương ứng)
Mà BE + EA = AB; CD + DA = AC
AB = AC (tam giác ABC cân tại A)
Suy ra EA = DA ⇒ ∆AED cân tại A ⇒ (tính chất)
Mà (tổng ba góc của một tam giác)
Suy ra (1)
Có mà (tổng ba góc của một tam giác)
Suy ra (1)
Từ (1) và (2) suy ra mà hai góc đồng vị nên ED // BC.
Suy ra (hai góc so le trong)
Mà (chứng ninh trên)
Suy ra
Do đó tam giác EBD cân tại E (dấu hiệu nhận biết)
Suy ra EB = ED
Vậy BE = CD = ED.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. ∆AMB = ∆AMC;
B. M là trung điểm của BC;
C. HK // BC;
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
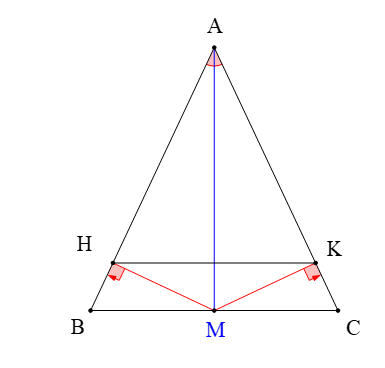
Ta có ∆ABC cân tại A (giả thiết) suy ra AB = AC; (tính chất)
Xét ∆AMB và ∆AMC có:
AB = AC
(vì AM là tia phân giác góc BAC)
Suy ra ∆AMB = ∆AMC (g.c.g)
Do đó: BM = MC (hai cạnh tương ứng) suy ra M là trung điểm của BC
Xét hai tam giác vuông AMH và AMK có:
AM là cạnh chung
Suy ra ∆AMH = ∆AMK (cạnh huyền – góc nhọn)
Do đó: AH = AK (hai cạnh tương ứng) suy ra ∆AHK cân tại A
⇒ (tính chất)
Mà (tổng ba góc của một tam giác)
Suy ra (1)
Có mà (tổng ba góc của một tam giác)
Suy ra (1)
Từ (1) và (2) suy ra mà hai góc đồng vị nên HK // BC.
Vì ∆AMH = ∆AMK (chứng minh trên)
(hai góc tương ứng) suy ra MA là tia phân giác của góc HMK.
Vậy MA là tia phân giác của góc HMC là sai.
Câu 2
A. ∆DEF vuông;
B. ∆DEF vuông cân;
C. ∆DEF đều;
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
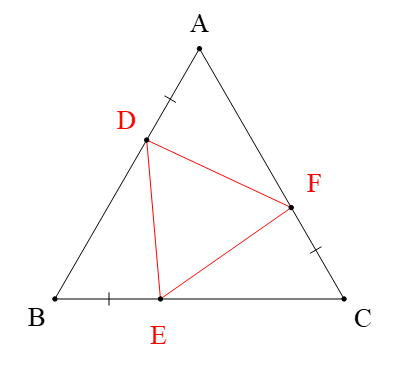
Ta có: ∆ABC đều (giả thiết) ⇒ AB = AC = BC và (tính chất)
Có AD + BD = AB; BE + EC = BC; CF + FA = AC
Mà AD = BE = CÂU: (giả thiết)
Nên BD = EC = FA
Xét ∆ADF và ∆BED có
AD = BE
FA = BD
Suy ra ∆ADF = ∆BED (c.g.c)
Do đó DF = ED (hai cạnh tương ứng) (1)
Xét ∆ADF và ∆CFE có
AD = CF
FA = EC
Suy ra ∆ADF = ∆ CFE (c.g.c)
Do đó DF = FE (hai cạnh tương ứng) (1)
Từ (1) và (2) suy ra DF = FE = ED
Do đó tam giác DFE đều.