Cho ∆ABC cân tại A có trực tâm I. Biết . Số đo các góc của ∆ABC là
Cho ∆ABC cân tại A có trực tâm I. Biết . Số đo các góc của ∆ABC là
A. ; ;
B. ; ;
C. ;
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Gọi BI cắt AC tại H, CI cắt AB tại K
⇒ BH, CK là đường cao của ∆ABC
Ta có (hai góc kề bù)
⇒
⇒
∆CIH vuông tại H ⇒
∆CKA vuông tại K ⇒
Do đó
⇒
Mà ∆ABC cân (giả thiết)
Suy ra ∆ABC đều
Do đó .
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. ;
B. ;
C. ;
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
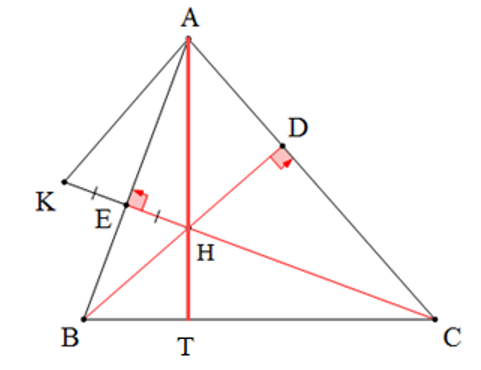
Gọi AH cắt BC tại T ⇒ AT là đường cao của ∆ABC.
Có AB là trung trực của HK (giả thiết) ⇒ KE = HE và AE ⊥ KH
Xét ∆AKE và ∆AHE có
AE là cạnh chung
KE = HE
Suy ra ∆AKE = ∆AHE (c.g.c)
Do đó (hai góc tương ứng)
Hay (1)
∆TAB vuông tại T ⇒
∆ECB vuông tại E ⇒
Do đó hay (2)
Từ (1) và (2) suy ra .
Câu 2
A. ∆MNP cân tại N;
B. ∆MEF cân tại E;
C. H là trọng tâm ∆MNP;
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
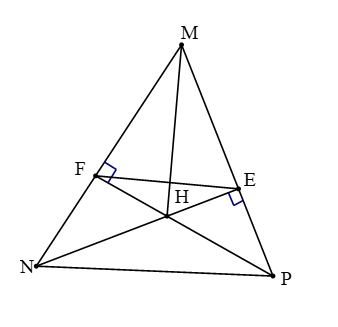
∆MNP có hai đường cao NE và PF cắt nhau tại H
⇒ H là trực tâm ∆MNP
⇒ MH ⊥ BC
Xét ∆MNE và ∆MPF có
NE = PF (giả thiết)
(cùng phụ góc M)
Suy ra ∆MNE = ∆MPF (g.c.g)
Do đó MN = MP (hai cạnh tương ứng) ⇒ ∆MNP cân tại M
ME = MF (hai cạnh tương ứng) ⇒ ∆MFE cân tại M.
Câu 3
A. BH là đường trung tuyến của ∆ABC;
B. BH là đường phân giác của ∆ABC;
C. BH là đường trung trực của ∆ABC;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 98°;
B. 108°;
C. 110°;
D. 70°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 10 cm;
B. 20 cm;
C. 25 cm;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 9 cm;
B. 18 cm;
C. 4,5 cm;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập