Cho ∆ABC vuông tại C, đường cao CD. Trên cạnh CD lấy M (M khác C và D). Qua M kẻ đường thẳng song song với BC cắt AB tại N. Khẳng định đúng là
Cho ∆ABC vuông tại C, đường cao CD. Trên cạnh CD lấy M (M khác C và D). Qua M kẻ đường thẳng song song với BC cắt AB tại N. Khẳng định đúng là
A. M là trọng tâm ∆ABC;
B. M là trực tâm ∆ABC;
C. MA = MB = MC;
D. M là trực tâm ∆ACN.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
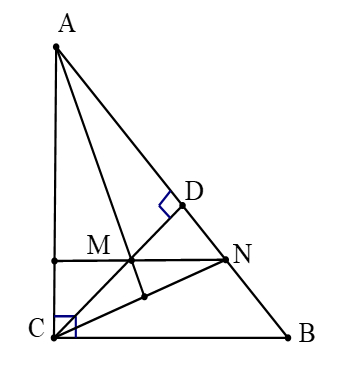
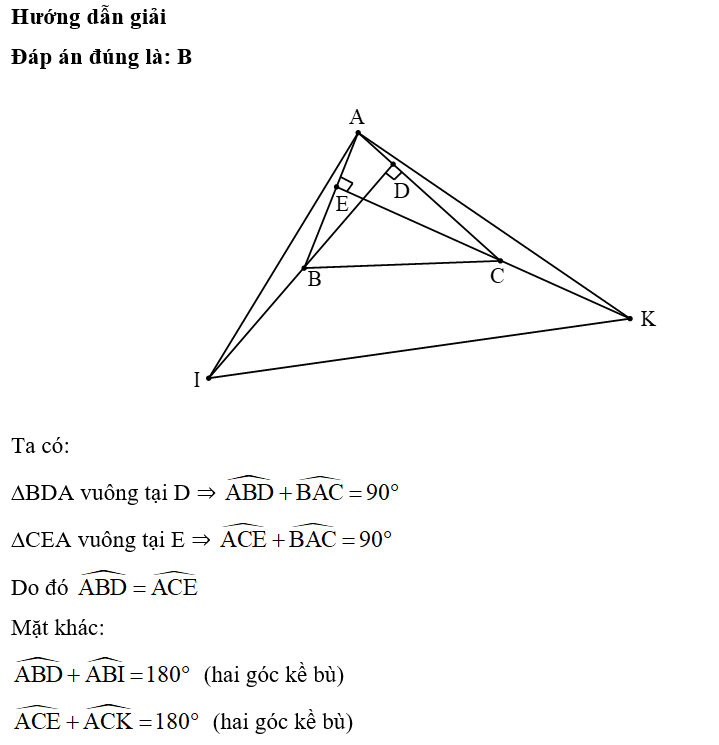
CD là đường cao của ∆ABC ⇒ CD ⊥ AB hay CD ⊥ AN
∆ABC vuông tại C (giả thiết) ⇒ BC ⊥ AC
Mà MN // BC (giả thiết)
Do đó MN ⊥ AC
Xét ∆CAN có:
NM và CD là đường cao và chúng cắt nhau tại M
Do đó M là trực tâm của ∆CAN.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
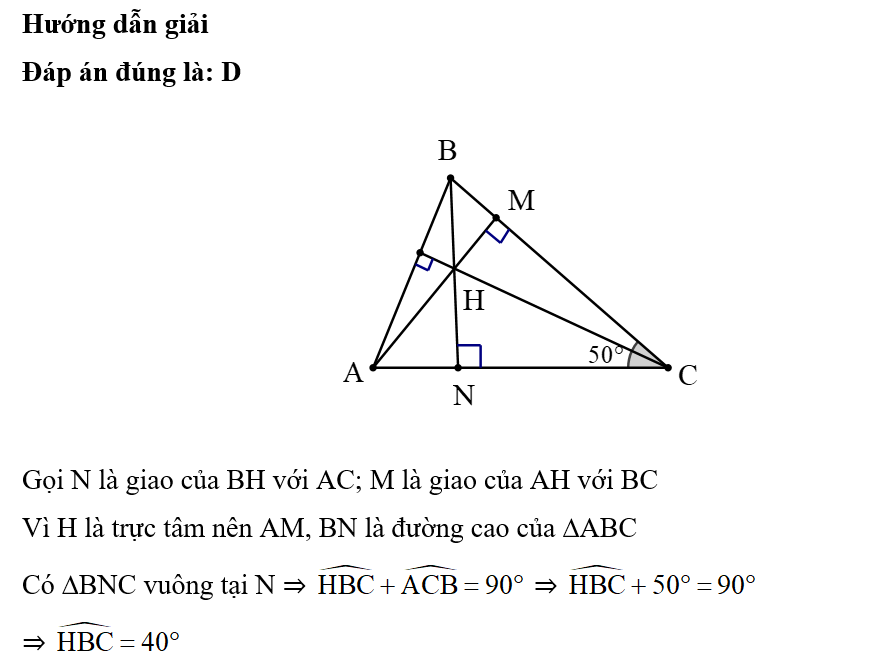
Câu 2
A. ∆AIK cân tại A;
B. ∆AIK vuông cân tại A;
C. ∆AIK đều;
D. ∆AIK vuông tại A.
Lời giải
Nhắn tin Zalo