Cho ∆ABC có . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?
Cho ∆ABC có . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?
A. Trung trực của EF đi qua A;
B. BE + CF = BC;
C. ;
D. Cả A, B và C đều sai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
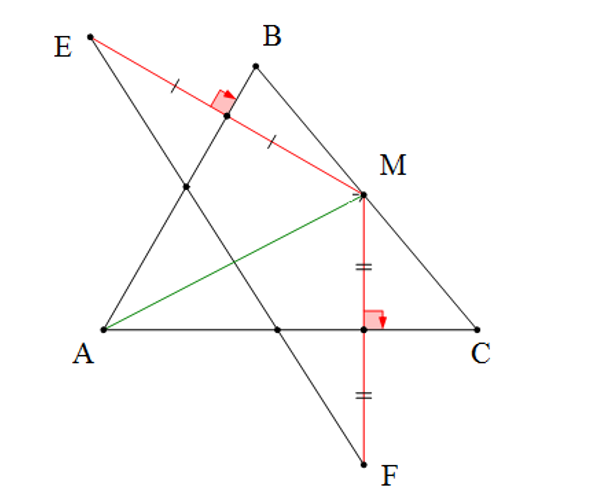
+) Ta có AB là trung trực của ME (giả thiết) ⇒ AE = AM (tính chất đường trung trực)
AC là trung trực của MF (giả thiết) ⇒ AF = AM (tính chất đường trung trực)
Do đó AE = AF ⇒ A thuộc đường trung trực của EF
Hay trung trực của EF đi qua A.
+) Ta có: B thuộc đường trung trực của ME ⇒ BE = BM (tính chất đường trung trực)
C thuộc đường trung trực của MF ⇒ CF = CM (tính chất đường trung trực)
Mà BM + CM = BC
Nên BE + CF = BC
+) Xét ∆AEB và ∆AMB có
AE = AM
AB là cạnh chung
EB = MB
Suy ra ∆AEB = ∆AMB (c.c.c)
⇒ (hai góc tương ứng)
Xét ∆AFC và ∆AMC có
AF = AM
AC là cạnh chung
FC = MC
Suy ra ∆AFC = ∆AMC (c.c.c)
⇒ (hai góc tương ứng)
Ta có:
⇒ .
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. AE;
B. DC;
C. ED;
D. ED và DC.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
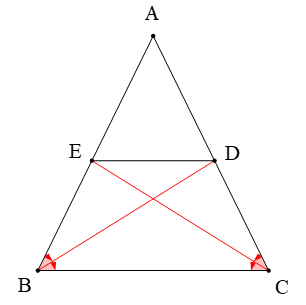
Ta có ∆ABC cân tại A (giả thiết) suy ra (tính chất)
BD là tia phân giác góc B nên
CE là tia phân giác góc C nên
Do đó
Xét ∆BEC và ∆CDB có:
BC là cạnh chung
(chứng minh trên)
Suy ra ∆BEC = ∆CDB (g.c.g)
Do đó BE = CD (hai cạnh tương ứng)
Mà BE + EA = AB; CD + DA = AC
AB = AC (tam giác ABC cân tại A)
Suy ra EA = DA ⇒ ∆AED cân tại A ⇒ (tính chất)
Mà (tổng ba góc của một tam giác)
Suy ra (1)
Có mà (tổng ba góc của một tam giác)
Suy ra (1)
Từ (1) và (2) suy ra mà hai góc đồng vị nên ED // BC.
Suy ra (hai góc so le trong)
Mà (chứng ninh trên)
Suy ra
Do đó tam giác EBD cân tại E (dấu hiệu nhận biết)
Suy ra EB = ED
Vậy BE = CD = ED.
Câu 2
A. ∆OBM = ∆OMA;
B. ;
C. ∆OBM = ∆OBA;
D. OM là tia phân giác của góc .
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
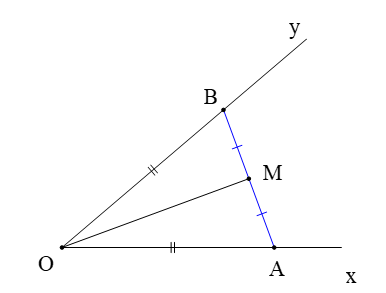
M là trung điểm của AB (giả thiết) nên MB = MA
Xét ∆OBM và ∆OMA có
OB = OA (giả thiết)
OM là cạnh chung
MB = MA (chứng minh trên)
Suy ra ∆OBM = ∆OAM (c.c.c)
Do đó (hai góc tương ứng)
(hai góc tương ứng)
Suy ra OM là tia phân giác góc BOA hay góc xOy.
Câu 3
A. ∆AIK cân tại A;
B. ∆AIK vuông cân tại A;
C. ∆AIK đều;
D. ∆AIK vuông tại A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Tam giác OBC cân;
B. OH ≠ OK;
C. AO là tia phân giác góc A;
D. OP = OQ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. BD = CE;
B. BE = CD;.
C. BK = KC;
D. DK = KC
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. ;
B. ;
C. ;
D. Không đủ dữ kiện để so sánh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập