Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
b) \[\sin x - \sqrt 3 \cos x = \sqrt 3 \]
Phương pháp:
Chia cả hai vế của phương trình cho \[\sqrt {{a^2} + {b^2}} \]
Cách giải:
\[\sin x - \sqrt 3 \cos x = \sqrt 3 \Leftrightarrow \frac{1}{2}\sin x - \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 3 }}{2}\]
\[ \Leftrightarrow \sin x\cos \frac{\pi }{3} - \cos x\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\]
\[ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{3} = \frac{\pi }{3} + k2\pi \\x - \frac{\pi }{3} = \frac{{2\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = \pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
a, b) Xác định 2 điểm chung của hai mặt phẳng.
c) Sử dụng định lí Ta-lét.
Cách giải:
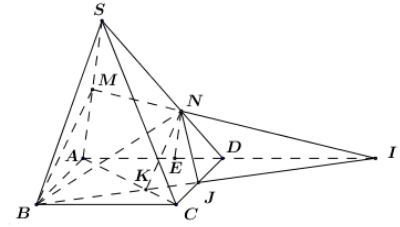
a) Xét \[\left( {BMN} \right)\] và \[\left( {ABCD} \right)\] có:
+ B là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}I \in MN \subset \left( {BMN} \right) \Rightarrow I \in \left( {BMN} \right)\\I \in AD \subset \left( {ABCD} \right) \Rightarrow I \in \left( {ABCD} \right)\end{array} \right. \Rightarrow I \in \left( {BMN} \right) \cap \left( {ABCD} \right) \Rightarrow I\] là điểm chung thứ hai.
Vậy \[\left( {BMN} \right) \cap \left( {ABCD} \right) = BI\]
b) Xét \[\left( {BMN} \right)\] và \[\left( {SCD} \right)\] có:
+ N là điểm chung thứ nhất.
+ \[J = BI \cap CD \Rightarrow \left\{ \begin{array}{l}J \in BI \subset \left( {BMN} \right) \Rightarrow J \in \left( {BMN} \right)\\J \in CD \subset \left( {SCD} \right) \Rightarrow J \in \left( {SCD} \right)\end{array} \right. \Rightarrow J \in \left( {BMN} \right) \cap \left( {SCD} \right) \Rightarrow J\] là điểm chung thứ hai.
Vậy \[\left( {BMN} \right) \cap \left( {SCD} \right) = NJ\]. Từ đó ta có thiết diện của hình chóp cắt bởi \[\left( {BMN} \right)\] là tứ giác BMNJ.
c) Trong \[\left( {SAD} \right)\] kẻ \[NE\parallel SA\left( {E \in AD} \right)\] ta có: \[\frac{{NE}}{{SA}} = \frac{{DN}}{{SD}} = \frac{1}{3} \Rightarrow \frac{{NE}}{{2MA}} = \frac{1}{3} \Leftrightarrow \frac{{NE}}{{MA}} = \frac{2}{3}\].
Mà \[\frac{{NE}}{{MA}} = \frac{{IN}}{{IM}} \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3} \Rightarrow \frac{{NI}}{{MN}} = 2\]
Mà IM là trung tuyến của tam giác \[SAI \Rightarrow N\] là trọng tâm tam giác SAI.
\[ \Rightarrow D\] là trung điểm của \[AI \Rightarrow \frac{{ID}}{{IA}} = \frac{1}{2} = \frac{{DJ}}{{AB}} = \frac{{DJ}}{{CD}} \Rightarrow J\] là trung điểm của CD.
\[ \Rightarrow \frac{{CJ}}{{AB}} = \frac{1}{2} = \frac{{KJ}}{{KB}} \Rightarrow KJ = \frac{1}{2}KB \Rightarrow IK = KJ + IJ = \frac{1}{2}KB + \frac{3}{2}KB = 2KB\]
Vậy \[\frac{{IN}}{{MN}} = \frac{{IK}}{{BK}} = 2 \Rightarrow BM\parallel KN\] (đpcm).
Câu 2
Lời giải
Đáp án C
Phương pháp:
+ Xác định điểm I.
+ Xác định thiết diện.
+ Sử dụng công thức He-rong để tính diện tích tam giác: \[{S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \].
Cách giải:
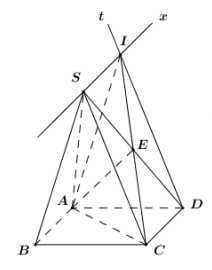
Trong \[\left( {SCD} \right)\] kẻ \[Dt\parallel SC\]
Ta có \[\left\{ \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\\left( {SAB} \right) \supset AB,\left( {SCD} \right) \supset CD\\AB\parallel CD\left( {gt} \right)\end{array} \right. \Rightarrow \] Giao tuyến của \[\left( {SAB} \right),\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD. Trong \[\left( {SAB} \right)\] kẻ \[Sx\parallel AB \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = Sx\]
Trong \[\left( {SCD} \right)\] gọi \[I = Dt \cap Sx\] ta có: \[\left\{ \begin{array}{l}I \in Dt\\I \in Sx \subset \left( {SAB} \right) \Rightarrow I \in \left( {SAB} \right)\end{array} \right. \Rightarrow I = Dt \cap \left( {SAB} \right)\].
Trong \[\left( {SCD} \right)\] gọi \[E = CI \cap SD\], khi đó thiết diện của chóp cắt bởi \[\left( {AIC} \right)\] là tam giác AEC.
ABCD là hình vuông cạnh \[a \Rightarrow AC = a\sqrt 2 \].
Dễ dàng chứng minh được SBAI, SCDI là hình bình hành \[ \Rightarrow AI = SB = a,E\] là trung điểm của SD, IC.
Tam giác SAD có \[SA = AD = a,\angle SAD = 90^\circ \Rightarrow \Delta SAD\] vuông cân tại \[A \Rightarrow SD = SA\sqrt 2 = a\sqrt 2 \].
\[ \Rightarrow AE = \frac{1}{2}SD = \frac{{a\sqrt 2 }}{2}\]
Xét tam giác IAC có:
\[A{E^2} = \frac{{A{I^2} + A{C^2}}}{2} - \frac{{I{C^2}}}{4} \Leftrightarrow \frac{{{a^2}}}{2} = \frac{{{a^2} + 2{a^2}}}{2} - \frac{{I{C^2}}}{4}\]
\[ \Rightarrow \frac{{I{C^2}}}{4} = {a^2} \Leftrightarrow I{C^2} = 4{a^2} \Leftrightarrow IC = 2a \Rightarrow EC = \frac{1}{2}IC = a\]
Khi đó áp dụng công thức Hê-rông ta có: \[{S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \frac{{{a^2}\sqrt 7 }}{8}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.