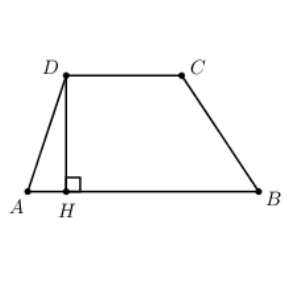
Hình thang ABCD có đáy \[AB = 2CD\], trong đó A, B thuộc trục hoành C, D thuộc đồ thị hàm số \[y = \cos x\]. Biết đường cao của hình thang ABCD bằng \[\frac{{\sqrt 3 }}{2}\] và \[AB < \pi \]. Tính độ dài cạnh đáy AB ?

Phương pháp:

a) Một đường thẳng song song với một mặt phẳng khi nó song song với một đường nằm trong mặt phẳng đó.

b) Xác định điểm chung của SD với \[\left( {BEF} \right),\] từ đó xác định thiết diện.

c) Xác định \[\left( \alpha \right).\] Sử dụng định lí Ta-lét.

Cách giải:

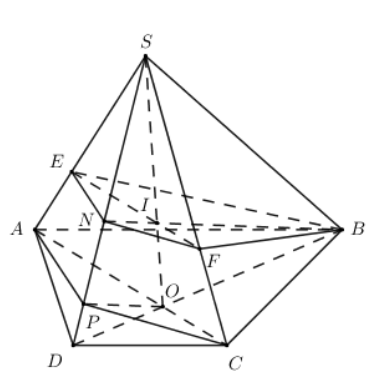
Ta có \[\left\{ \begin{array}{l}\left( {BEF} \right) \cap \left( {SAB} \right) = BE\\\left( {BEF} \right) \cap \left( {SAD} \right) = EN\\\left( {BEF} \right) \cap \left( {SCD} \right) = NF\\\left( {BEF} \right) \cap \left( {SBC} \right) = FB\end{array} \right. \Rightarrow \] Thiết diện của hình chóp cắt bởi mặt phẳng \[\left( {BEF} \right)\] là tứ giác BENF.

c) Ta có AC qua O và \[AC{\rm{ // }}EF \Rightarrow AC \subset \left( \alpha \right).\]

Trong \[\left( {SAD} \right)\] qua A kẻ \[AP{\rm{ // }}EN\left( {P \in SD} \right) \Rightarrow AP{\rm{ // }}\left( {BEF} \right) \Leftrightarrow AP \subset \left( \alpha \right).\]

Khi đó ta có \[\left( \alpha \right) \equiv \left( {BEF} \right).\]

Ta có \[\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SBD} \right) = OP\\\left( {BEF} \right) \cap \left( {SBD} \right) = BN\\\left( \alpha \right){\rm{ // }}\left( {BEF} \right)\end{array} \right. \Rightarrow OP{\rm{ // }}BN.\]

Áp dụng đinh lí Ta-lét ta có: \[\frac{{DP}}{{DN}} = \frac{{DO}}{{DB}}.\]

Ta có: \[\frac{{DO}}{{OB}} = \frac{{DC}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{DO}}{{DB}} = \frac{1}{3} \Rightarrow \frac{{DP}}{{DN}} = \frac{1}{3} \Rightarrow \frac{{DP}}{{PN}} = \frac{1}{2} \Rightarrow DP = \frac{1}{2}NP.\]

Lại áp dụng định lí Ta-lét ta có: \[\frac{{SN}}{{SP}} = \frac{{SE}}{{SA}} = \frac{2}{3}\left( {AP{\rm{ // }}EN} \right) \Rightarrow \frac{{SN}}{{NP}} = 2 \Rightarrow SN = 2NP.\]

Từ đó ta có \[\frac{{SP}}{{SD}} = \frac{{SN + NP}}{{SN + NP + DP}} = \frac{{2NP + NP}}{{2NP + NP + \frac{1}{2}NP}} = \frac{{3NP}}{{\frac{7}{2}NP}} = \frac{6}{7}.\]

Vậy \[\frac{{SP}}{{SD}} = \frac{6}{7}.\]

Đáp án B

Phương pháp:

Sử dụng công thức SHTQ của CSC: \[{u_n} = {u_1} + \left( {n - 1} \right)d.\]

Cách giải:

Giả sử 2018 là số hạng thứ n ta có \[{u_n} = 2018 \Leftrightarrow 2 + \left( {n - 1} \right)9 = 2018 \Leftrightarrow n = 225.\]