Cho tứ diện ABCD có \(AB = x\) thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.
Cho tứ diện ABCD có \(AB = x\) thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.
D. \(\frac{{a\sqrt 6 }}{3}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Cách giải:
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD))
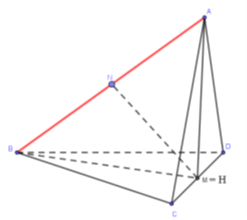
\( \Rightarrow H \in BM,\,\,\,AH \bot HM\)
\({V_{ABCD}}\) lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M
Hai tam giác ACD, BCD đều, cạnh a, có đường cao AM, BM bằng \(\frac{{a\sqrt 3 }}{2}\)
Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB \( \Rightarrow MN \bot AB\)
Mà \(MN \subset \left( {AMB} \right) \bot CD \Rightarrow MN \bot CD \Rightarrow \) MN là đoạn vuông góc chung của AB và CD
Khoảng cách giữa hai đường thẳng AB và CD là: \(MN = \frac{{AM}}{{\sqrt 2 }} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\sqrt 2 }} = \frac{{a\sqrt 6 }}{4}\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
D. 1
Lời giải
Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và điểm không xác định của y’
- Tính các giá trị tại \(\frac{1}{{{e^2}}}\), tại , tại nghiệm của y’ . Tìm GTLN, GTNN trong các giá trị đó. e
- Tính tích M.m.
Cách giải:
TXĐ: \(D = \left( {0; + \infty } \right)\)
\(y = x.\ln x \Rightarrow y' = \ln x + x.\frac{1}{x} = \ln x + 1\)
\(y' = 0 \Leftrightarrow x = \frac{1}{e}\)
Ta có: \(f\left( {\frac{1}{{{e^2}}}} \right) = - \frac{2}{{{e^2}}},\,\,\,f\left( e \right) = e,\,\,\,f\left( {\frac{1}{e}} \right) = - \frac{1}{e}\)
Vậy \(\mathop {\min }\limits_{\left[ {\frac{1}{{{e^2}}};e} \right]} f\left( x \right) = - \frac{1}{e} = m,\,\,\,\mathop {\max }\limits_{\left[ {\frac{1}{{{e^2}}};e} \right]} f\left( x \right) = e = M \Rightarrow M.m = - 1\)
Câu 2
D. \(\left[ {{{50}^0};{{70}^0}} \right)\)
Lời giải
Đáp án D
Phương pháp:
Tính thể tích của khối lăng trụ đứng, có đáy là hình thang cân mà hai cạnh bên bằng đáy bé và bằng 20cm.
Thể tích lớn nhất khi diện tích của hình thang cân lớn nhất.
Cách giải:
Thể tích nước lớn nhất khi diện tích của hình thang cân lớn nhất
Gọi độ dài đường cao là h. Khi đó, \(AE = BF = h\), từ đó, suy ra \(DE = CF = \sqrt {{{20}^2} - {h^2}} = \sqrt {400 - {h^2}} \)
\(CD = DE + EF + FC = 2\sqrt {400 - {h^2}} + 20\)
Diện tích hình thang: \(S = \left( {AB + CD} \right).AE:2 = \frac{{20 + 2\sqrt {400 - {h^2}} + 20}}{2}.h = 20h + h\sqrt {400 - {h^2}} \)
\(S' = 20 + \sqrt {400 - {h^2}} - h.\frac{h}{{\sqrt {400 - {h^2}} }} = 20 + \frac{{400 - 2{h^2}}}{{\sqrt {400 - {h^2}} }}\)
\(S' = 0 \Leftrightarrow 20\sqrt {400 - {h^2}} + 400 - {2^2} = 0 \Leftrightarrow {h^2} = 300 \Rightarrow h = 10\sqrt 3 \)
Bảng xét dấu:
Diện tích hình thang lớn nhất khi \(h = 10\sqrt 3 \)
Khi đó, \(\sin \varphi = \frac{{10\sqrt 3 }}{0} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = {60^0} \Rightarrow \varphi \in \left[ {{{50}^0};{{70}^0}} \right)\)
Câu 3
A. Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
B. Hàm số nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
D. Hàm số đồng biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(c > b > a\)
B. \(c > a > b\)
C. \(a > b > c\)
D. \(b > a > c\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(y' = e.\ln x + x\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. \(\left( {0;1} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. \(m \in \mathbb{R}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập