Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là 30cm, 20cm và 30cm (như hình vẽ). Một con kiến xuất phát từ điểm A muốn tới điểm B thì quãng đường ngắn nhất nó phải đi là bao nhiêu cm?
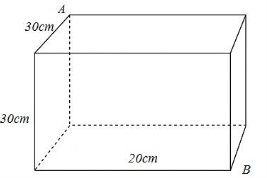
Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là 30cm, 20cm và 30cm (như hình vẽ). Một con kiến xuất phát từ điểm A muốn tới điểm B thì quãng đường ngắn nhất nó phải đi là bao nhiêu cm?
B. \(10\sqrt {34} \,cm\)
D. \(20 + 30\sqrt 2 \,cm\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
Trải tất cả các mặt của hình hộp chữ nhật ra cùng một mặt phẳng.
Cách giải:
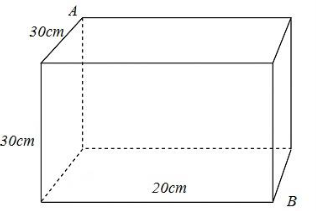
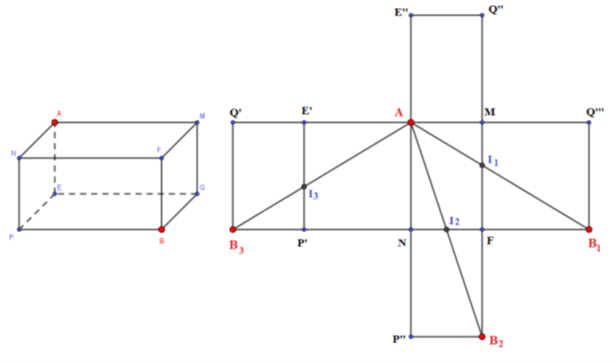
Để đến được B, đầu tiên con kiến phải đi trên một trong các mặt bên và đi đến một trong các cạnh bên: NP, PE, QE, MQ, MF, NF
* Giả sử con kiến đi đến I trên cạnh MF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài \(AB = \sqrt {A{Q^2} + Q{B^2}} = \sqrt {{{50}^2} + {{30}^2}} = 10\sqrt {34} \left( {cm} \right)\)
* Giả sử con kiến đi đến I trên cạnh NF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài \(AB = \sqrt {A{P^2} + P{B^2}} = \sqrt {{{60}^2} + {{20}^2}} = 20\sqrt {10} \left( {cm} \right)\)
* Giả sử con kiến đi đến I trên cạnh PF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài \(AB = \sqrt {A{N^2} + N{B^2}} = \sqrt {{{30}^2} + {{50}^2}} = 10\sqrt {34} \left( {cm} \right)\)
Vậy, quãng đường ngắn nhất con kiến đi là \(10\sqrt {34} \left( {cm} \right)\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
D. 1
Lời giải
Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và điểm không xác định của y’
- Tính các giá trị tại \(\frac{1}{{{e^2}}}\), tại , tại nghiệm của y’ . Tìm GTLN, GTNN trong các giá trị đó. e
- Tính tích M.m.
Cách giải:
TXĐ: \(D = \left( {0; + \infty } \right)\)
\(y = x.\ln x \Rightarrow y' = \ln x + x.\frac{1}{x} = \ln x + 1\)
\(y' = 0 \Leftrightarrow x = \frac{1}{e}\)
Ta có: \(f\left( {\frac{1}{{{e^2}}}} \right) = - \frac{2}{{{e^2}}},\,\,\,f\left( e \right) = e,\,\,\,f\left( {\frac{1}{e}} \right) = - \frac{1}{e}\)
Vậy \(\mathop {\min }\limits_{\left[ {\frac{1}{{{e^2}}};e} \right]} f\left( x \right) = - \frac{1}{e} = m,\,\,\,\mathop {\max }\limits_{\left[ {\frac{1}{{{e^2}}};e} \right]} f\left( x \right) = e = M \Rightarrow M.m = - 1\)
Câu 2
D. \(\left[ {{{50}^0};{{70}^0}} \right)\)
Lời giải
Đáp án D
Phương pháp:
Tính thể tích của khối lăng trụ đứng, có đáy là hình thang cân mà hai cạnh bên bằng đáy bé và bằng 20cm.
Thể tích lớn nhất khi diện tích của hình thang cân lớn nhất.
Cách giải:
Thể tích nước lớn nhất khi diện tích của hình thang cân lớn nhất
Gọi độ dài đường cao là h. Khi đó, \(AE = BF = h\), từ đó, suy ra \(DE = CF = \sqrt {{{20}^2} - {h^2}} = \sqrt {400 - {h^2}} \)
\(CD = DE + EF + FC = 2\sqrt {400 - {h^2}} + 20\)
Diện tích hình thang: \(S = \left( {AB + CD} \right).AE:2 = \frac{{20 + 2\sqrt {400 - {h^2}} + 20}}{2}.h = 20h + h\sqrt {400 - {h^2}} \)
\(S' = 20 + \sqrt {400 - {h^2}} - h.\frac{h}{{\sqrt {400 - {h^2}} }} = 20 + \frac{{400 - 2{h^2}}}{{\sqrt {400 - {h^2}} }}\)
\(S' = 0 \Leftrightarrow 20\sqrt {400 - {h^2}} + 400 - {2^2} = 0 \Leftrightarrow {h^2} = 300 \Rightarrow h = 10\sqrt 3 \)
Bảng xét dấu:
Diện tích hình thang lớn nhất khi \(h = 10\sqrt 3 \)
Khi đó, \(\sin \varphi = \frac{{10\sqrt 3 }}{0} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = {60^0} \Rightarrow \varphi \in \left[ {{{50}^0};{{70}^0}} \right)\)
Câu 3
A. Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
B. Hàm số nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
D. Hàm số đồng biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
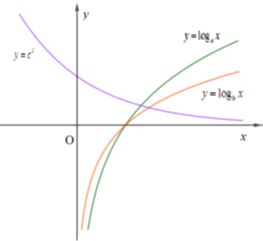
A. \(c > b > a\)
B. \(c > a > b\)
C. \(a > b > c\)
D. \(b > a > c\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(y' = e.\ln x + x\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. \(\left( {0;1} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. \(m \in \mathbb{R}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập