Ông An gửi 100 triệu đồng vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất năm. Sau 5 năm ông rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại ông tiếp tục gửi vào ngân hàng với kỳ hạn và lãi suất như lần trước. Số tiền lãi mà ông An nhận được sau 10 năm gửi gần nhất với giá trị nào sau đây? 8%/

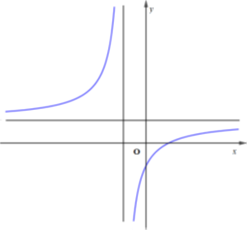
A. \(a > 0,\,\,b < 0,\,\,c > 0\)

B. \(a > 0,\,\,b > 0,\,\,c < 0\)

C. \(a > 0,\,\,b < 0,\,\,c < 0\)

D. \(a < 0,\,\,b > 0,\,\,c > 0\)

D. \(y = {x^5} + {x^3} - 1\)

D. \(V = \frac{{\sqrt 3 {a^3}}}{2}\)

D. \(\int {\sin 2xdx = 2\cos 2x + C} \)

A. \(y = {x^3} - 3{x^2} + 2\)

B. \(y = {x^3} + 3{x^2} + 2\)

C. \(y = - {x^3} + 3{x^2} + 2\)

D. \(y = - {x^3} + 6{x^2} + 2\)

B. \[\int {f\left( x \right)dx = \ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \]

D. \[\int {f\left( x \right)dx = \frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \]

A. Đồ thị các hàm số \(y = {a^x}\) và \(y = {\left( {\frac{1}{a}} \right)^{x\,}}\,\,\,0 < a \ne 1\) đối xứng nhau qua trục tung.

B. Hàm số \(y = {a^{x\,}}\,\,\,0 < a \ne 1\) đồng biến trên \(\mathbb{R}\)

C. Hàm số \(y = {a^{x\,}}\,\,\,a > 1\) nghịch biến trên \(\mathbb{R}\)

D. Đồ thị hàm số \(y = {a^{x\,}}\,\,\,0 < a \ne 1\) luôn đi qua điểm có tọa độ \(\left( {a;1} \right)\)