Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 (tiếp theo) - Đề 28 có đáp án
23 người thi tuần này 4.6 9.4 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
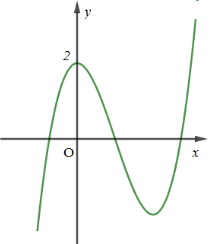
Câu 1
A. \(y = {x^3} - 3{x^2} + 2\)
B. \(y = {x^3} + 3{x^2} + 2\)
C. \(y = - {x^3} + 3{x^2} + 2\)
D. \(y = - {x^3} + 6{x^2} + 2\)
Lời giải
Đáp án A
Phương pháp:
Nhận dạng đồ thị hàm số bậc ba
Cách giải:
Quan sát đồ thị hàm số ta thấy khi \(x \to + \infty \) thì \(y \to + \infty \) nên hệ số \(a > 0 \Rightarrow \) Loại phương án C và D
Mặt khác đồ thị hàm số đạt cực trị tại hai điểm: \(x = 0\) và \(x = {x_0} > 0\)
Xét \(y = {x^3} + 3{x^2} + 2 \Rightarrow y' = 3{x^2} + 6x,\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2 < 0\end{array} \right. \Rightarrow \) Loại phương án B
Ta chọn phương án A.
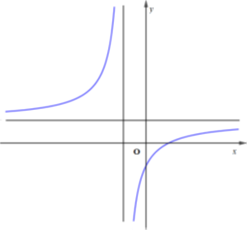
Câu 2
A. \(a > 0,\,\,b < 0,\,\,c > 0\)
B. \(a > 0,\,\,b > 0,\,\,c < 0\)
C. \(a > 0,\,\,b < 0,\,\,c < 0\)
D. \(a < 0,\,\,b > 0,\,\,c > 0\)
Lời giải
Đáp án C
Phương pháp:
Đồ thị hàm số \(y = \frac{{ax + b}}{{x - c}}\) có hai đường tiệm cận: \(x = c\) và \(y = a\), đồng thời cắt trục hoành tại điểm \(\left( { - \frac{b}{a};0} \right)\)
Cách giải:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng \(x = {x_0} < 0 \Rightarrow c < 0\), đồ thị hàm số có tiệm cận ngang \(y = {y_0} > 0 \Rightarrow a > 0\)
Đồ thị hàm số cắt trục hoành tại điểm\(\left( {x{'_0};0} \right),\,\,x{'_0} > 0 \Rightarrow - \frac{b}{a} > 0\)
Mà \(a > 0 \Rightarrow b < 0\)
Vậy \(a > 0,\,\,b < 0,\,\,c < 0\)
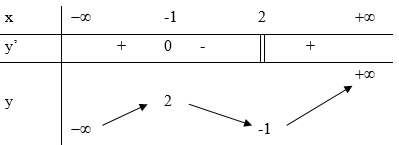
Câu 3
A. Đường thẳng \(y = 2\) là đường tiệm cận đứng của đồ thị hàm số.
B. Hàm số không có giá trị nhỏ nhất.
C. Hàm số có một điểm cực trị.
D. Hàm số nghịch biến trên \(\mathbb{R}\).
Lời giải
Đáp án B
Phương pháp:
Hàm bậc nhất trên bậc nhất luôn đơn điệu trên từng khoảng xác định của nó.
Cách giải:
Hàm số bậc nhất trên bậc nhất không có giá trị nhỏ nhất.
Câu 4
A. 1
B. 0
C. 3
D. 2
Lời giải
Đáp án D
Phương pháp:
Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành đồ giao điểm của hai hàm số đó.
Cách giải:
Xét phương trình hoành độ giao điểm: \(x + \frac{2}{{x - 1}} = 2x,\,\,\,x \ne 1\)
\( \Leftrightarrow \frac{2}{{x - 1}} = x \Leftrightarrow 2 = {x^2} - x \Rightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\)
\( \Rightarrow \) Số giao điểm của hai đồ thị hàm số là 2.
Câu 5
D. \(V = \frac{{2\sqrt 3 }}{3}{a^3}\)
Lời giải
Đáp án C
Phương pháp:
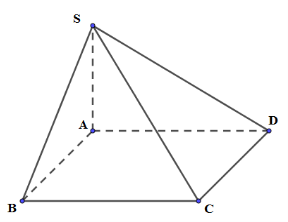
Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}S.h\)
Với: S là diện tích của đáy,
h là chiều cao của khối chóp.
Cách giải:.
Xét tam giác vuông ABC có: \(BC\sqrt {5{a^2} - {a^2}} = 2a\)
\(V = \frac{1}{3}S.h = \frac{1}{3}.a.2a.\sqrt 2 a = \frac{{2\sqrt 2 }}{3}{a^3}\)
Câu 6
D. \(M = 0\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
D. \(1\,\,v\`a \,\,\frac{1}{2} + \ln 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
D. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
D. \(V = \frac{{3{a^3}}}{4}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
D. \(V = 6{a^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
D. \(\overrightarrow u //\overrightarrow v \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
B. A, B, C thẳng hàng.
D. O, A, B, C là 4 đỉnh của một hình tứ diện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
D. \(\frac{{2\sqrt 5 }}{5}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
D. \(y = {x^5} + {x^3} - 1\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
B. \({\log _{{a^\alpha }}}b = \alpha {\log _a}b\)
D. \({\log _a}bc = {\log _a}b + {\log _a}c\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. Tâm mặt cầu ngoại tiếp hình chóp trùng với đỉnh S.
B. Tâm mặt cầu ngoại tiếp hình chóp là tâm của mặt đáy ABCD.
C. Tâm mặt cầu ngoại tiếp hình chóp là trung điểm của đoạn thẳng nối S với tâm của mặt đáy ABCD.
D. Tâm mặt cầu ngoại tiếp hình chóp là trọng tâm tam giác SAC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
D. \(V = \frac{{\sqrt 3 {a^3}}}{2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. Đồ thị các hàm số \(y = {a^x}\) và \(y = {\left( {\frac{1}{a}} \right)^{x\,}}\,\,\,0 < a \ne 1\) đối xứng nhau qua trục tung.
B. Hàm số \(y = {a^{x\,}}\,\,\,0 < a \ne 1\) đồng biến trên \(\mathbb{R}\)
C. Hàm số \(y = {a^{x\,}}\,\,\,a > 1\) nghịch biến trên \(\mathbb{R}\)
D. Đồ thị hàm số \(y = {a^{x\,}}\,\,\,0 < a \ne 1\) luôn đi qua điểm có tọa độ \(\left( {a;1} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
D. \(y = 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
D. 46,933 triệu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
D. \(y' = 1 + \ln x\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
D. \(P = {x^{\frac{4}{5}}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
B. Điểm cực đại của đồ thị hàm số là \(\left( { - 1;2} \right)\)
D. Hàm số đạt cực đại tại điểm \(x = - 1\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
D. \(\int {\sin 2xdx = 2\cos 2x + C} \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. 0
B. 1
C. 3
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
D. \(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow 0 \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
D. \(S = \left( { - 1;3} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
D. \({120^0}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
D. \(\left[ {2;3} \right]\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
D. 4 máy
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
D. \(V = \frac{{\sqrt {15} {a^3}}}{2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
D. \(\ln 3\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
B. \[\int {f\left( x \right)dx = \ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \]
D. \[\int {f\left( x \right)dx = \frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
D. \(m = 4\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
B. \(F\left( x \right) = {\frac{{\ln \left| {2x + 3} \right|}}{4}^2} + 3\)
D. \(F\left( x \right) = \frac{{\ln \left| {x + \frac{3}{2}} \right|}}{2} + 4\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
B. \(F\left( x \right) = x\sin x + \cos \,x + C\)
D. \(F\left( x \right) = - x\sin x + \cos \,x + C\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
A. Diện tích toàn phần của hình trụ bằng \(2\pi rh + \pi {r^2} + \pi {h^2}\)
C. Thể tích của khối trụ bằng \(\pi {r^2}h\)
D. Khoảng cách giữa trục của hình trụ và đường sinh của hình trụ bằng r.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
D. \(V = \frac{{128\sqrt {78} }}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
D. \(\frac{{\sqrt {31} a}}{{32}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
D. \(\frac{{\sqrt {13} r}}{{20}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
D. \(\left[ \begin{array}{l}m < - 2\\m > 2\end{array} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.