Cho hàm số liên tục trên khoảng \(\left( {a;b} \right)\) và \({x_0} \in \left( {a;b} \right)\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm \({x_0}\) khi và chỉ khi \(f'\left( {{x_0}} \right) = 0\).
(2) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm và có đạo hàm cấp hai tại điểm \({x_0}\) thỏa mãn điều kiện \(f'\left( {{x_0}} \right) = f''\left( {{x_0}} \right) = 0\) thì điểm \({x_0}\) không phải là điểm cực trị của hàm số \(y = f\left( x \right)\).
(3) Nếu \(f'\left( x \right)\) đổi dấu khi x qua điểm \({x_0}\) thì điểm \({x_0}\) là điểm cực tiểu của hàm số \(y = f\left( x \right)\)
(4) Nếu hàm số \(y = f\left( x \right)\)có đạo hàm và có đạo hàm cấp hai tại điểm \({x_0}\) thỏa mãn điều kiện \(f'\left( {{x_0}} \right) = 0,\,\,\,f''\left( {{x_0}} \right) > 0\) thì điểm \({x_0}\) là điểm cực tiểu của hàm số \(y = f\left( x \right)\).
Cho hàm số liên tục trên khoảng \(\left( {a;b} \right)\) và \({x_0} \in \left( {a;b} \right)\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm \({x_0}\) khi và chỉ khi \(f'\left( {{x_0}} \right) = 0\).
(2) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm và có đạo hàm cấp hai tại điểm \({x_0}\) thỏa mãn điều kiện \(f'\left( {{x_0}} \right) = f''\left( {{x_0}} \right) = 0\) thì điểm \({x_0}\) không phải là điểm cực trị của hàm số \(y = f\left( x \right)\).
(3) Nếu \(f'\left( x \right)\) đổi dấu khi x qua điểm \({x_0}\) thì điểm \({x_0}\) là điểm cực tiểu của hàm số \(y = f\left( x \right)\)
(4) Nếu hàm số \(y = f\left( x \right)\)có đạo hàm và có đạo hàm cấp hai tại điểm \({x_0}\) thỏa mãn điều kiện \(f'\left( {{x_0}} \right) = 0,\,\,\,f''\left( {{x_0}} \right) > 0\) thì điểm \({x_0}\) là điểm cực tiểu của hàm số \(y = f\left( x \right)\).
A. 1
B. 2
C. 0
D. 3
Quảng cáo
Trả lời:
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số \(y = {x^3}\) có \(y' = 3{x^2} = 0 \Leftrightarrow x = 0\). Tuy nhiên \(x = 0\) không là điểm cực trị của hàm số.
(2) sai, khi \(f''\left( {{x_0}} \right) = 0\), ta không có kết luận về điểm \({x_0}\) có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(a > 0,\,\,b < 0,\,\,c > 0\)
B. \(a > 0,\,\,b > 0,\,\,c < 0\)
C. \(a > 0,\,\,b < 0,\,\,c < 0\)
D. \(a < 0,\,\,b > 0,\,\,c > 0\)
Lời giải
Đáp án C
Phương pháp:
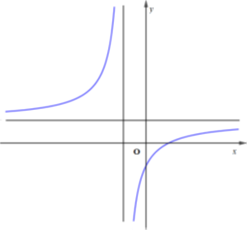
Đồ thị hàm số \(y = \frac{{ax + b}}{{x - c}}\) có hai đường tiệm cận: \(x = c\) và \(y = a\), đồng thời cắt trục hoành tại điểm \(\left( { - \frac{b}{a};0} \right)\)
Cách giải:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng \(x = {x_0} < 0 \Rightarrow c < 0\), đồ thị hàm số có tiệm cận ngang \(y = {y_0} > 0 \Rightarrow a > 0\)
Đồ thị hàm số cắt trục hoành tại điểm\(\left( {x{'_0};0} \right),\,\,x{'_0} > 0 \Rightarrow - \frac{b}{a} > 0\)
Mà \(a > 0 \Rightarrow b < 0\)
Vậy \(a > 0,\,\,b < 0,\,\,c < 0\)
Câu 2
D. \(y = {x^5} + {x^3} - 1\)
Lời giải
Đáp án A
Phương pháp:
* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
- Bước 1: Tìm tập xác định, tính \(f'\left( x \right)\)
- Bước 2: Tìm các điểm tại đó \(f'\left( x \right) = 0\) hoặc \(f'\left( x \right)\) không xác định
- Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
+) \(y = \frac{{x - 1}}{{x + 2}}\) ta có \(y' = \frac{{2 + 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{3}{{{{\left( {x + 2} \right)}^2}}} > 0,\,\,\forall x \ne - 2 \Rightarrow \) Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right);\,\,\,\left( { - 2; + \infty } \right)\)
+) \(y = {x^3} + 2 \Rightarrow y' = 3{x^2} \ge 0,\,\,\forall x \in \mathbb{R}\): Hàm số đồng biến trên \(\mathbb{R}\).
+) \(y = x + 1 \Rightarrow y' = 1 > 0,\,\,\forall x \in \mathbb{R}\): Hàm số đồng biến trên \(\mathbb{R}\).
+) \(y = {x^5} + {x^3} - 1 \Rightarrow y' = 5{x^4} + 3{x^2} \ge 0,\,\,\forall x \in \mathbb{R};\,\,\,y' = 0 \Leftrightarrow x = 0 \Rightarrow \) Hàm số đồng biến trên \(\mathbb{R}\).
Câu 3
D. \(V = \frac{{\sqrt 3 {a^3}}}{2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
B. \[\int {f\left( x \right)dx = \ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \]
D. \[\int {f\left( x \right)dx = \frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(\int {\sin 2xdx = 2\cos 2x + C} \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
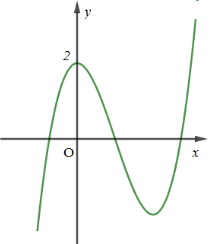
A. \(y = {x^3} - 3{x^2} + 2\)
B. \(y = {x^3} + 3{x^2} + 2\)
C. \(y = - {x^3} + 3{x^2} + 2\)
D. \(y = - {x^3} + 6{x^2} + 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Đồ thị các hàm số \(y = {a^x}\) và \(y = {\left( {\frac{1}{a}} \right)^{x\,}}\,\,\,0 < a \ne 1\) đối xứng nhau qua trục tung.
B. Hàm số \(y = {a^{x\,}}\,\,\,0 < a \ne 1\) đồng biến trên \(\mathbb{R}\)
C. Hàm số \(y = {a^{x\,}}\,\,\,a > 1\) nghịch biến trên \(\mathbb{R}\)
D. Đồ thị hàm số \(y = {a^{x\,}}\,\,\,0 < a \ne 1\) luôn đi qua điểm có tọa độ \(\left( {a;1} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.