Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 (tiếp theo) - Đề 36 có đáp án
20 người thi tuần này 4.6 9.5 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
B. \( - 2 < m < 2\)
D. \( - 2 < m < 3\)
Lời giải
Đáp án A
Phương pháp:
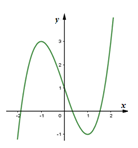
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3x\) và đường thẳng \(y = m\)
Cách giải:
Ta có: \({x^3} - 3x - m = 0 \Leftrightarrow {x^3} - 3x = m\,\,\left( 1 \right)\)
Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3x\) và đường thẳng \(y = m\)
Quan sát đồ thị hàm số, ta thấy: để đồ thị hàm số \(y = {x^3} - 3x\) cắt đường thẳng \(y = m\) tại 3 điểm phân biệt thì \( - 1 < m < 3\).
Vậy để phương trình đã cho có ba nghiệm phân biệt thì \( - 1 < m < 3\)
Lời giải
Đáp án A
Phương pháp:
Xác định số điểm mà tại đó đạo hàm \(f'\left( x \right)\) đổi dấu.
Cách giải:
\(f'\left( x \right) = {x^2}{\left( {x + 1} \right)^2}\left( {2x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = \frac{1}{2}\end{array} \right.\)
Trong đó \(f'\left( x \right)\) chỉ đổi dấu tại điểm \(x = \frac{1}{2} \Rightarrow \) Hàm số đã cho có 1 điểm cực trị.
Câu 3
D. \(\left( { - \infty ;0} \right),\,\left( {2; + \infty } \right)\)
Lời giải
Đáp án B
Phương pháp:
Xác định khoảng mà \(y' \ge 0\), (\(y' = 0\)tại hữu hạn điểm trên khoảng đó)
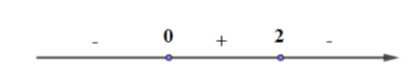
Cách giải:
\(y = - {x^3} + 3{x^2} + 5 \Rightarrow y' = - 3{x^2} + 6x\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right. \Rightarrow \) Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\)
Cách giải:
\(y = - {x^3} + 3{x^2} + 5 \Rightarrow y' = - 3{x^2} + 6x\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right. \Rightarrow \) Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\)
Câu 4
Lời giải
Đáp án C
Phương pháp:
Hàm số bậc ba đạt cực đại tại điểm\(x = {x_0} \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.\)
Cách giải:
Ta có: \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + m\)
\( \Rightarrow y' = 3{x^2} - 6mx + 3{m^2} - 3\)
\(y'' = 6x - 6\)
Hàm số đạt cực đại tại \(x = 1 \Leftrightarrow \left\{ \begin{array}{l}y'\left( 1 \right) = 0\\y''\left( 1 \right) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3 - 6m + 3{m^2} - 3 = 0\\6 - 6m < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\\m > 1\end{array} \right. \Leftrightarrow m = 2\)
Câu 5
D. \(\left( { - \infty ; - \frac{{25}}{{12}}} \right]\)
Lời giải
Đáp án D
Phương pháp:
Hàm số \(y = f\left( x \right)\) đồng biến trên R \( \Leftrightarrow f'\left( x \right) \ge 0\,\,\forall x \in R\) và bằng 0 tại hữu hạn điểm.
Cách giải:
\(y = {x^3} + 5{x^2} - 4mx - 3 \Rightarrow y' = 3{x^2} + 10x - 4m\)
Hàm số đồng biến trên R \[ \Leftrightarrow y' \ge 0,\,\,\forall x \in \,R \Leftrightarrow 3{x^2} + 10x - 4m \ge 0,\,\,\forall x \in \,R \Leftrightarrow \left\{ \begin{array}{l}3 > 0\\\Delta ' \le 0\end{array} \right.\]
\( \Leftrightarrow 25 + 12m \le 0 \Leftrightarrow m \le - \frac{{25}}{{12}}\)
Câu 6
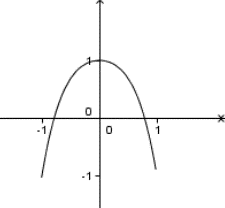
B. \(y = - {x^4} + {x^2} + 1\)
D. \({x^4} - {x^2} + 1\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
B. \(y = - {x^3} + 9{x^2} + 3x + 2\)
D. \(y = {x^3} - 9{x^2} - 3x + 5\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
B. nghịch biến trên \(R\backslash \left\{ 1 \right\}\)
D. nghịch biến trên từng khoảng xác định.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
D. \(y = x + 1\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
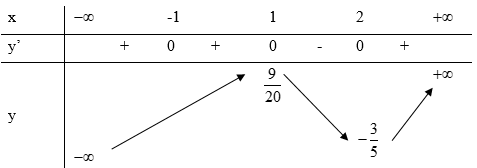
A. Hàm số có ba cực trị.
B. Hàm số có giá trị lớn nhất bằng \(\frac{9}{{20}}\) và giá trị nhỏ nhất bằng \( - \frac{3}{5}\).
C. Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\).
D. Hàm số đạt cực đại tại \(x = 2\) và đạt cực tiểu tại \(x = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
D. \( - 4\sqrt 2 \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
D. 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
D. \({x^m}:{x^n} = {x^{m - n}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
D. \(y = {x^{\frac{5}{6}}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
D. \(28\sqrt 3 \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
D. \(1 - x\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
D. \(R\backslash \left( {1;2} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
D. \(\frac{1}{4}\left( {6a - 1} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
D. \(x = \frac{1}{e}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
D. \(\left( {\frac{1}{2};14} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
D. \(\frac{{{a^3}}}{6}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
D. \(\frac{{\sqrt 2 {a^3}}}{6}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
D. \(V = \frac{{14\pi \sqrt {14} .{a^3}}}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
D. \(3\sqrt 2 {a^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
B. Mọi tứ diện luôn có mặt cầu ngoại tiếp.
C. Mọi hình chóp luôn có mặt cầu ngoại tiếp.
D. Mọi hình hộp chữ nhật luôn có mặt cầu ngoại tiếp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
D. \(26\pi {a^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
D. \(8\pi {a^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
D. \(10\pi \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
D. \(\frac{{\pi \sqrt 2 .{a^3}}}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
D. \(\frac{{{a^3}.\sqrt 6 }}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
D. \(\left[ {\frac{1}{2};\frac{{e + 1}}{2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
B. có tiệm cận ngang \(y = \frac{5}{2}\)
D. không có tiệm cận ngang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
D. \(32\pi {a^3}\sqrt 2 \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
D. \(m = 25\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
D. \(\left( {0;2} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 41
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
D. \(m = 1\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 43
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 45
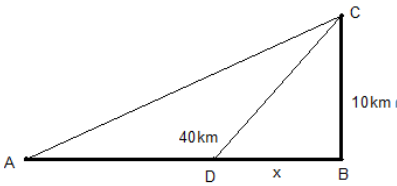
D. \(40\,km\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
D. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
D. \(\frac{{x\sqrt {3 - {x^2}} }}{6}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
B. \(\frac{{V'}}{V} = \frac{{{a^2}}}{{{a^2} + {b^2} + {c^2}}}\)
D. \(\frac{{V'}}{V} = \frac{{{a^2}}}{{{a^2} + {b^2}}} + \frac{{{a^2}}}{{{a^2} + {b^2} + {c^2}}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
D. \(\frac{1}{{18}}{a^2}.\sqrt {{b^2} - \frac{{{a^2}}}{2}} \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
D. \(h = r\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.