Câu hỏi:
23/02/2023 2,545
Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là BC = 10km, khoảng cách từ khách sạn A đến điểm ngắn nhất tính từ đảo C vào bờ là AB = 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy từ khách sạn ra đảo (như hình vẽ dưới đây). Biết kinh phí đi đường thủy là 5 USD/km, kinh phí đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một đoạn AD bao nhiêu để kinh phí đi từ A đến C nhỏ nhất? (AB vuông góc BC-hình dưới đây)
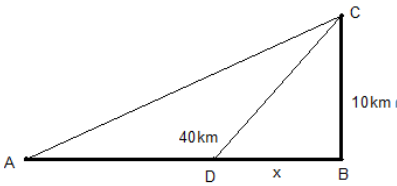
Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là BC = 10km, khoảng cách từ khách sạn A đến điểm ngắn nhất tính từ đảo C vào bờ là AB = 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy từ khách sạn ra đảo (như hình vẽ dưới đây). Biết kinh phí đi đường thủy là 5 USD/km, kinh phí đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một đoạn AD bao nhiêu để kinh phí đi từ A đến C nhỏ nhất? (AB vuông góc BC-hình dưới đây)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
Phương pháp:
Lập hàm số tính kinh phí đi từ A đến C, với ẩn \(x = BD\)
Cách giải:
Gọi độ dài đoạn BD là \(x\left( {km} \right),\,\,\left( {x \in \left[ {0;40} \right]} \right)\)
Khi đó \(AD = 40 - x,\,\,DC = \sqrt {100 + {x^2}} \left( {km} \right)\)
Kinh phí đi từ A đến C: \(y = f\left( x \right) = 3\left( {40 - x} \right) + 5\sqrt {100 + {x^2}} \)
\(f'\left( x \right) = - 3 + \frac{{5x}}{{\sqrt {100 + {x^2}} }} = \frac{{ - 3\sqrt {100 + {x^2}} + 5x}}{{\sqrt {100 + {x^2}} }}\)
\(f'\left( x \right) = 0 \Leftrightarrow 3\sqrt {100 + {x^2}} = 5x \Leftrightarrow 900 + 9{x^2} = 25{x^2} \Leftrightarrow 16{x^2} = 900 \Leftrightarrow x = \frac{{15}}{2}\)
Ta có \(f\left( 0 \right) = 170,\,\,f\left( {40} \right) = 50\sqrt {17} ,\,\,\,f\left( {\frac{{15}}{2}} \right) = 160\)
Vậy, kinh phí đi từ A đến C nhỏ nhất bằng 160USD khi \(BD = x = \frac{{15}}{2}\left( {km} \right)\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
Phương pháp:
Hàm số \(y = {\log _a}f\left( x \right)\,\left( {0 < a \ne 1} \right)\) xác định \( \Leftrightarrow f\left( x \right) > 0\)
Cách giải:
ĐKXĐ: \({x^2} - 3x + 2 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < 1\end{array} \right. \Rightarrow \) TXĐ: \(D = R\backslash \left[ {1;2} \right]\)
Lời giải
Đáp án A
Phương pháp:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3x\) và đường thẳng \(y = m\)
Cách giải:
Ta có: \({x^3} - 3x - m = 0 \Leftrightarrow {x^3} - 3x = m\,\,\left( 1 \right)\)
Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3x\) và đường thẳng \(y = m\)
Quan sát đồ thị hàm số, ta thấy: để đồ thị hàm số \(y = {x^3} - 3x\) cắt đường thẳng \(y = m\) tại 3 điểm phân biệt thì \( - 1 < m < 3\).
Vậy để phương trình đã cho có ba nghiệm phân biệt thì \( - 1 < m < 3\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận