khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

20/02/2023 332 Lưu

Cho hình chóp đều \[S.ABC\] có cạnh đáy bằng \[a\], cạnh bên bằng \[\frac{{a\sqrt {21} }}{6}\]. Tính theo \(a\) thể tích \(V\) của khối chóp \[S.ABC\].

A.\[V = \frac{{{a^3}\sqrt 3 }}{{12}}\].
B. \[V = \frac{{{a^3}\sqrt 3 }}{8}\].
C. \[V = \frac{{{a^3}\sqrt 3 }}{6}\].
D. \[V = \frac{{{a^3}\sqrt 3 }}{{24}}\].
Xem lời giải

Câu hỏi trong đề: Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack
Lời giải

Chọn D

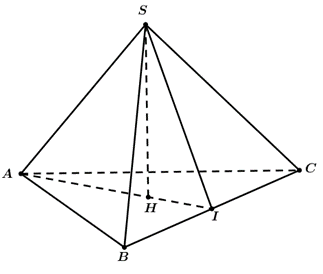
Media VietJack

Gọi \[I\] là trung điểm của cạnh \[BC\], \[H\] là trọng tâm của tam giác \[ABC\] ta có: \[SH \bot \left( {ABC} \right)\] và\[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {S{A^2} - {{\left( {\frac{2}{3}AI} \right)}^2}} = \sqrt {{{\left( {\frac{{a\sqrt {21} }}{6}} \right)}^2} - {{\left( {\frac{2}{3}.\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}.\]

Vậy \[V = \frac{1}{3}.SH.{S_{\Delta ABC}} = \frac{1}{3}.\frac{a}{2}.\frac{1}{2}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{24}}.\]

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đạo hàm \[f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\]. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng nào dưới đây?
A.\(\left( { - \infty \,;\, - 1} \right)\).
B. \(\left( { - 1\,;\,1} \right)\).
C. \(\left( {2\,;\, + \infty } \right)\).
D. \(\left( {1\,;\,2} \right)\).

Lời giải

Lời giải

Chọn D

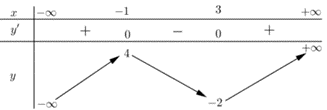
Ta có \[f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right) \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.\].

Từ đó, ta có bảng biến thiên như sau:

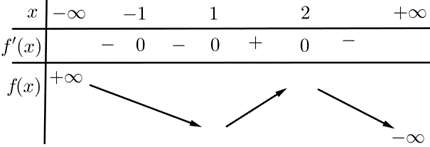
Media VietJack

Dựa vào bảng biến thiên thì hàm số \[y = f\left( x \right)\] đồng biến trên \(\left( {1\,;\,2} \right)\).

Câu 2

Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như hình vẽ.

Media VietJack

Khẳng định nào sau đây đúng?
A. \(ab < 0\); \(ac < 0\).
B. \(bd < 0\); \(bc > 0\).
C. \(ad > 0\); \(bd > 0\).
D. \(ab < 0\); \(ad > 0\).

Lời giải

Lời giải

Chọn D

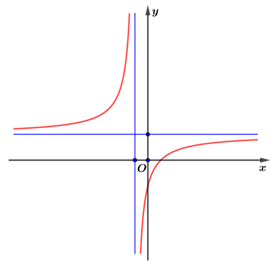
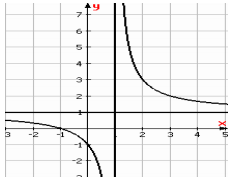
Đồ thị hàm số \[y = \frac{{ax + b}}{{cx + d}}\] đi qua \(M\left( {0\,;\,\frac{b}{d}} \right)\), có đường tiệm cận đứng \(x = - \frac{d}{c}\), đường tiệm cận ngang \(y = \frac{a}{c}\).

Quan sát đồ thị thấy:

+ Giao điểm với trục tung nằm phía dưới \(Ox\)nên \(\frac{b}{d} < 0 \Leftrightarrow bd < 0\)\( \Rightarrow \) Loại phương án

+ Đường tiệm cận ngang nằm phía trên \(Ox\)nên \(\frac{a}{c} > 0 \Leftrightarrow ac > 0\)\( \Rightarrow \) Loại phương án

+ Đường tiệm cận đứng nằm bên trái \(Oy\)nên \( - \frac{d}{c} < 0 \Leftrightarrow cd > 0\).

Ta có: \(\left\{ \begin{array}{l}bd < 0\\cd > 0\end{array} \right. \Rightarrow bc < 0\)\( \Rightarrow \) Loại phương án

Kiểm chứng phương án D: \(\left\{ \begin{array}{l}ac > 0\\cd > 0\end{array} \right. \Rightarrow ad > 0\); \(\left\{ \begin{array}{l}ad > 0\\bd < 0\end{array} \right. \Rightarrow ab < 0\).

Lưu ý: Có thể sử dụng giao điểm của đồ thị với trục hoành nằm bên phải \(Oy\)nên \( - \frac{b}{a} > 0 \Leftrightarrow ab < 0\).

Câu 3

Cho hình thang cân có độ dài đáy nhỏ và hai cạnh bên đều bằng \(1\) mét. Khi đó hình thang đã cho có diện tích lớn nhất bằng?
A. \(3\sqrt 3 \left( {{m^2}} \right)\).
B. \(\frac{{3\sqrt 3 }}{2}\left( {{m^2}} \right)\).
C. \(\frac{{3\sqrt 3 }}{4}\left( {{m^2}} \right)\).
D. \(1\left( {{m^2}} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm tất cả các giá trị thực của tham số \[m\] để hàm số \[y = \frac{1}{3}{x^3} - \left( {2m - 1} \right){x^2} + \left( {{m^2} - m + 7} \right)x + m - 5\] có hai điểm cực trị là độ dài hai cạnh góc vuông của một tam giác vuông có cạnh huyền bằng \[\sqrt {74} \].
A. \[m = 3\].
B. \[\left[ \begin{array}{l}m = - 3\\m = 2\end{array} \right.\].
C. \[m = 2\].
D. \[\left[ \begin{array}{l}m = 3\\m = - 2\end{array} \right.\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Đồ thị sau đây là của hàm số nào?
Media VietJack
A. \(y = \frac{{x + 2}}{{1 - x}}\).
B. \(y = \frac{{x - 1}}{{x + 1}}\).
C. \(y = \frac{{x + 1}}{{x - 1}}\).
D. \(y = \frac{{2x - 1}}{{x - 1}}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên sau:

Media VietJack

Số nghiệm của phương trình \(f\left( x \right) - 2 = 0\)là
A. 3.
B. 2.
C. 1.
D. 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để hàm số \(y = {x^4} - 2m{x^2} + m + 1\mathord{\setbox0=\hbox{$\exists$}\rlap{\raise.2ex\hbox to\wd0{\hss/\hss}}\box0} \)có giá trị cực tiểu bằng \( - 1\). Tổng các phần tử thuộc \(S\)là:
A. \( - 2\).
B. \(0\).
C. \(1\).
D. \( - 1\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập