Cho hình chóp \(S.ABC\), \(M\)và \(N\) là các điểm thuộc các cạnh \(SA\) và \(SB\) sao cho \(MA = 2SM\), \(SN = 2NB\), \(\left( \alpha \right)\) là mặt phẳng qua \(MN\) và song song với \(SC\). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp \(S.ABC\) thành hai khối đa diện \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\) với \(\left( {{H_1}} \right)\) là khối đa diện chứa điểm \(S\), \(\left( {{H_2}} \right)\) là khối đa diện chứa điểm \(A\). Gọi \({V_1}\) và \({V_2}\) lần lượt là thể tích của \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
Câu hỏi trong đề: Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Chọn A
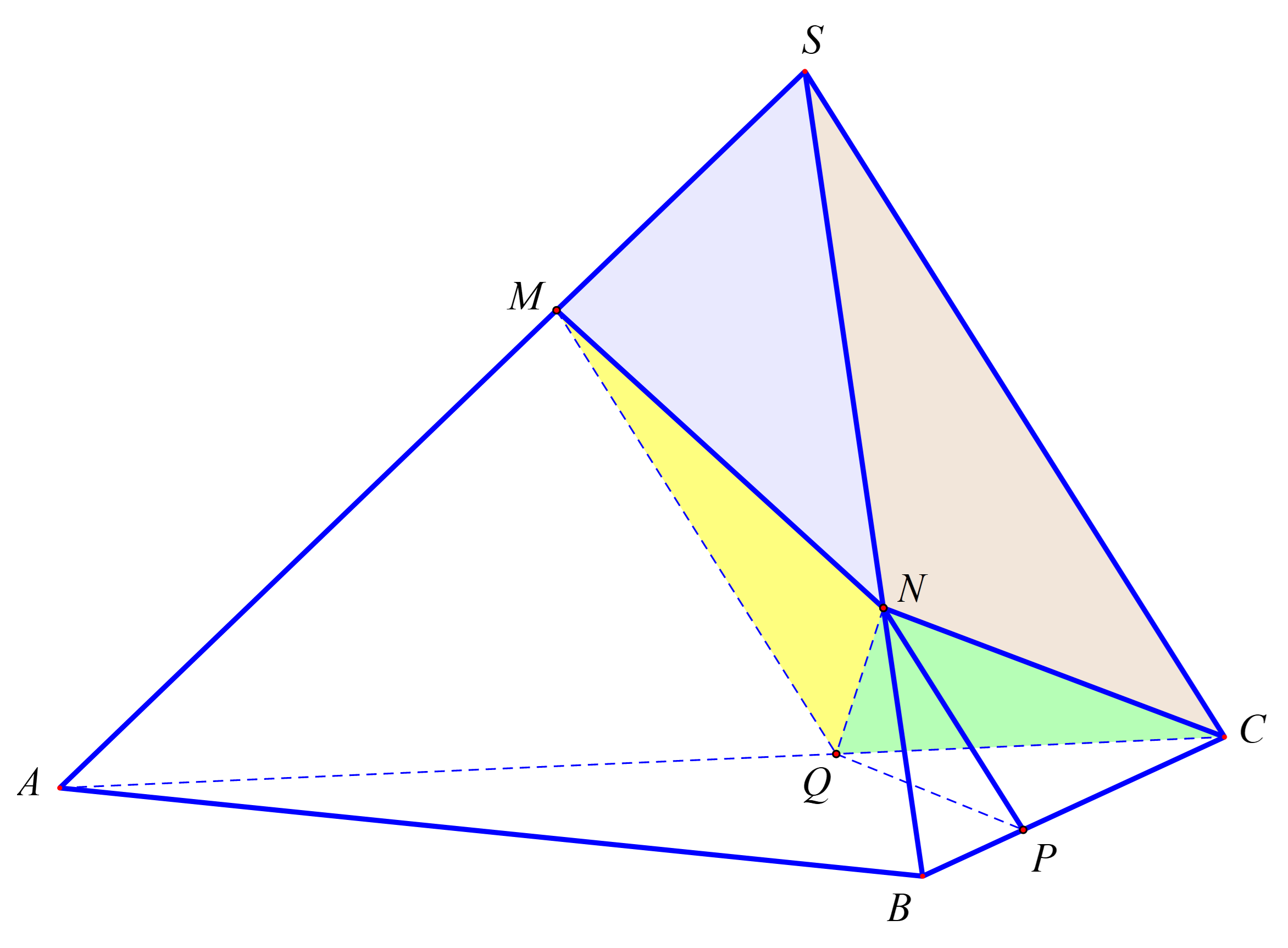
Kí hiệu \(V\) là thể tích khối tứ diện \(SABC\).
Gọi \(P\), \(Q\) lần lượt là giao điểm của \(\left( \alpha \right)\) với các đường thẳng \(BC\), \(AC\).
Ta có \(NP\;{\rm{//}}\;MQ\;{\rm{//}}\;SC\).
Khi chia khối \(\left( {{H_1}} \right)\) bởi mặt phẳng \(\left( {QNC} \right)\), ta được hai khối chóp \(N.SMQC\) và \(N.QPC\).
Ta có \(\frac{{{V_{N.SMQC}}}}{{{V_{B.ASC}}}} = \frac{{d\left( {N,\left( {SAC} \right)} \right)}}{{d\left( {B,\left( {SAC} \right)} \right)}} \cdot \frac{{{S_{SMQC}}}}{{{S_{SAC}}}}\).
\(\frac{{d\left( {N,\left( {SAC} \right)} \right)}}{{d\left( {B,\left( {SAC} \right)} \right)}} = \frac{{NS}}{{BS}} = \frac{2}{3}\); \(\frac{{{S_{AMQ}}}}{{{S_{ASC}}}} = \frac{{AM}}{{AS}}.\frac{{AQ}}{{AC}} = {\left( {\frac{{AM}}{{AS}}} \right)^2} = \frac{4}{9} \Rightarrow \frac{{{S_{SMQC}}}}{{{S_{ASC}}}} = \frac{5}{9}\).
Do đó \(\frac{{{V_{N.SMQC}}}}{{{V_{B.ASC}}}} = \frac{2}{3} \cdot \frac{5}{9} = \frac{{10}}{{27}}\).
\(\frac{{{V_{N.QPC}}}}{{{V_{S.ABC}}}} = \frac{{d\left( {N,\left( {QPC} \right)} \right)}}{{d\left( {S,\left( {ABC} \right)} \right)}} \cdot \frac{{{S_{QPC}}}}{{{S_{ABC}}}} = \frac{{NB}}{{SB}} \cdot \left( {\frac{{CQ}}{{CA}} \cdot \frac{{CP}}{{CB}}} \right) = \frac{1}{3} \cdot \left( {\frac{1}{3} \cdot \frac{2}{3}} \right) = \frac{2}{{27}}\).
Do đó \(\frac{{{V_1}}}{V} = \frac{{{V_{N.SMQC}}}}{{{V_{B.ASC}}}} + \frac{{{V_{N.QPC}}}}{{{V_{S.ABC}}}} = \frac{{10}}{{27}} + \frac{2}{{27}} = \frac{4}{9} \Rightarrow \frac{{{V_1}}}{{{V_1} + {V_2}}} = \frac{4}{9} \Rightarrow 5{V_1} = 4{V_2} \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{4}{5}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
Chọn D
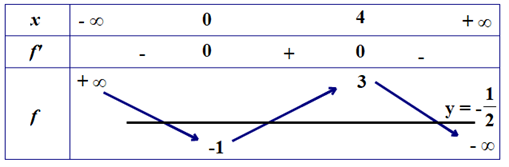
Vì \(f'\left( x \right) = - {x^2} - 1 < 0\), \(\forall x \in \mathbb{R}\) nên hàm số nghịch biến trên \(\mathbb{R}\).
Vì thế:
Do \(1 < 2\) nên \(f\left( 1 \right) > f\left( 2 \right)\). Suy ra A sai.
Do \(3 > 2\) nên \(f\left( 3 \right) < f\left( 2 \right)\). Suy ra B sai.
Do \(1 > 0\) nên \(f\left( 1 \right) < f\left( 0 \right)\). Suy ra C sai.
Do \(0 > - 1\) nên \(f\left( 0 \right) < f\left( { - 1} \right)\). Suy ra D đúng.
Câu 2
Lời giải
Lời giải
Chọn B
Hàm số \(y = {x^3} - 3x + 1 - m \Rightarrow y' = 3{x^2} - 3\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\).
Với \(x = 1 \Rightarrow y = - 1 - m\), với \(x = - 1 \Rightarrow y = 3 - m\)
Để hàm số có giá trị cực đại và giá trị cực tiểu trái dấu nhau khi và chỉ khi \(\left( { - 1 - m} \right)\left( {3 - m} \right) < 0 \Leftrightarrow - 1 < m < 3\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.