Hình chữ nhật A có chiều rộng 2x (cm), chiều dài gấp k (k > 1) lần chiều rộng. Hình chữ nhật B có chiều dài 3x (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì B phải có chiều rộng bằng bao nhiêu?
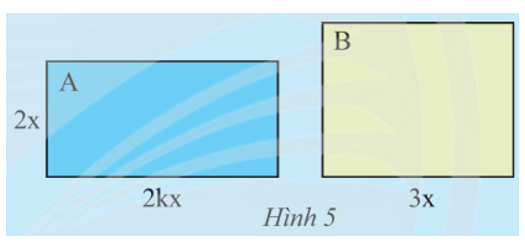
Hình chữ nhật A có chiều rộng 2x (cm), chiều dài gấp k (k > 1) lần chiều rộng. Hình chữ nhật B có chiều dài 3x (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì B phải có chiều rộng bằng bao nhiêu?

Quảng cáo
Trả lời:
Diện tích hình chữ nhật A là: SA = 2x.2kx = 4kx2 (cm2).
Gọi chiều rộng của hình chữ nhật B là R (cm).
Khi đó diện tích của hình chữ nhật B là: SB = R.3x (cm2).
Để hai hình chữ nhật này có diện tích bằng nhau thì SA = SB
Do đó 4kx2 = R.3x
Suy ra R = (4kx2) : (3x)
R = (4 : 3).k.(x2 : x) = kx (cm).
Vậy để hai hình chữ nhật này có diện tích bằng nhau thì chiều rộng của hình chữ nhật B là kx cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để đi được 1 km thì xuồng tiêu tốn lít dầu khi xuôi dòng và tiêu tốn lít dầu khi ngược dòng.
Số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B là:
(lít).
Số lít dầu mà xuồng tiêu tốn để đi từ bến B xuôi dòng quay lại bến A là:
(lít).
Biểu thức biểu thị số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A là: (lít).
Lời giải
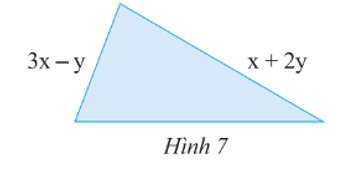
Độ dài cạnh còn thiếu của tam giác ở Hình 7 là:
(7x + 5y) – (3x – y) – (x + 2y)
= 7x + 5y – 3x + y – x – 2y
= (7x – 3x – x) + (5y + y – 2y)
= 3x + 4y.
Vậy độ dài cạnh còn thiếu của tam giác ở Hình 7 là 3x + 4y.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.