Câu hỏi trong đề: Giải SGK Toán 8 KNTT Bài 11. Hình thang cân có đáp án !!
Quảng cáo
Trả lời:
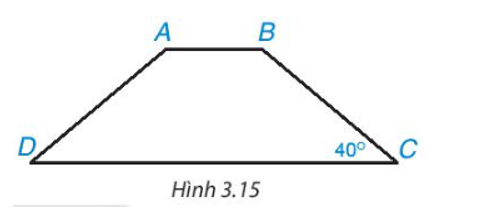
Để hình thang ABCD là hình thang cân thì .
Suy ra (không thỏa mãn định lí tổng bốn góc trong một tứ giác).
Khi đó, ACBD không phải là tứ giác.
Do đó ACBD cũng không phải là hình thang cân.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi O là giao điểm của AC và BD.
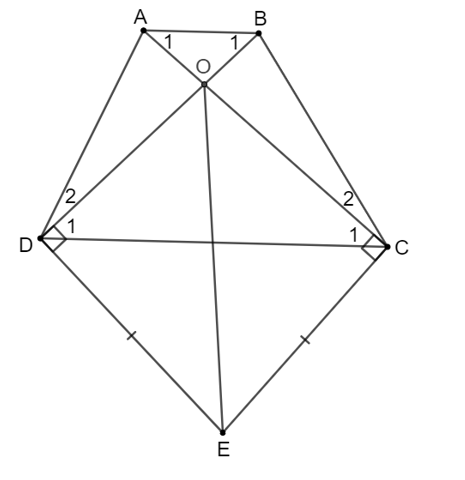
Xét ∆DOE và ∆COE có:
(vì OD ⊥ DE; OC ⊥ CE)
EC = ED (giả thiết)
Cạnh OE chung
Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).
Suy ra OC = OD (hai cạnh tương ứng).
Do đó tam giác OCD cân tại O nên .
Vì ABCD là hình thang nên AB // CD suy ra (cặp góc so le trong).
Do đó (vì ).
Suy ra tam giác OAB cân tại O nên OA = OB.
Xét ∆OAD và ∆OBC có:
OA = OB (chứng minh trên)
(hai góc đối đỉnh)
OC = OD (chứng minh trên)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra (hai góc tương ứng).
Ta có .
Mà nên .
Hình thang ABCD có nên ABCD là hình thang cân.
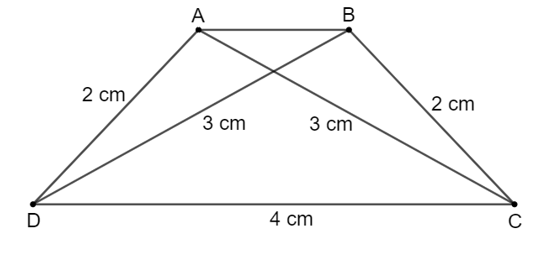
Lời giải
Cách vẽ hình thang cân ABCD có đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm:
- Vẽ cạnh CD = 4 cm.
- Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.
- Dùng compa vẽ hai đường tròn (C; 3 cm) và (D; 2 cm). Hai đường tròn này cắt nhau tại điểm B.
- Nối AB, AD, BC ta được hình thang ABCD (như hình vẽ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
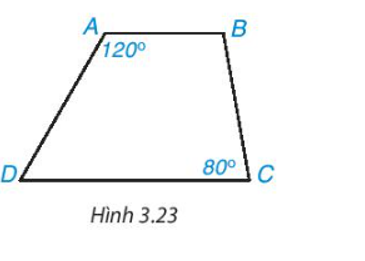
Quachthihongai@gmail.com Quach
Giải xàm
Xem tất cả 1 phản hồi
hildegard akaraxia
mk thấy dễ hiểu mà
Quachthihongai@gmail.com Quach
Giải khó hiểu, nên hiểu đề hơn