Toạ độ giao điểm của hai đường thẳng \({d_1}:y = \frac{{1 - 3x}}{4}\) và \({d_2}:y = - \left( {\frac{x}{3} + 1} \right)\) là:
A. (0; ‒1).
B. \(\left( { - \frac{7}{3};2} \right)\).
C. \(\left( {0;\frac{1}{4}} \right)\).
D. (3; ‒2).
Toạ độ giao điểm của hai đường thẳng \({d_1}:y = \frac{{1 - 3x}}{4}\) và \({d_2}:y = - \left( {\frac{x}{3} + 1} \right)\) là:
A. (0; ‒1).
B. \(\left( { - \frac{7}{3};2} \right)\).
C. \(\left( {0;\frac{1}{4}} \right)\).
D. (3; ‒2).
Quảng cáo
Trả lời:
Lời giải
Đáp án đúng là: D
Cách 1:
Giả sử điểm A(x0; y0) là giao điểm của d1 và d2.
Do A(x0; y0) thuộc d1 nên ta có \[{y_0} = \frac{{1 - 3{x_0}}}{4}\,\,\,\left( 1 \right)\]
Do A(x0; y0) thuộc d2 nên ta có \({y_0} = - \left( {\frac{{{x_0}}}{3} + 1} \right)\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có:
\[\frac{{1 - 3{x_0}}}{4} = - \left( {\frac{{{x_0}}}{3} + 1} \right)\]
Suy ra \[\frac{1}{4} - \frac{3}{4}{x_0} = - \frac{{{x_0}}}{3} - 1\]
Do đó \[ - \frac{3}{4}{x_0} + \frac{{{x_0}}}{3} = - 1 - \frac{1}{4}\]
Hay \[\frac{{ - 5}}{{12}}{x_0} = \frac{{ - 5}}{4}\]
Suy ra: x0 = 3
Thay x0 = 3 vào (1) ta có: \[{y_0} = \frac{{1 - 3.3}}{4} = \frac{{ - 8}}{4} = - 2\]
Vậy toạ độ giao điểm của hai đường thẳng d1 và d2 là: A(3; ‒2).
Cách 2:
• Xét điểm (0; ‒1)
Với x = 0, thay vào \(y = \frac{{1 - 3x}}{4}\) ta được \(y = \frac{1}{4}\), nên đường thẳng d1 không đi qua điểm (0; ‒1). Do đó phương án A là sai.
• Xét điểm \(\left( { - \frac{7}{3};2} \right)\)
Với \(x = - \frac{7}{3}\), thay vào \(y = \frac{{1 - 3x}}{4}\) ta được \(y = \frac{{1 - 3.\left( { - \frac{7}{3}} \right)}}{4} = \frac{{1 + 7}}{4} = \frac{8}{4} = 2\), nên đường thẳng d1 đi qua điểm \(\left( { - \frac{7}{3};2} \right)\).
Với \(x = - \frac{7}{3}\), thay vào \(y = - \left( {\frac{x}{3} + 1} \right)\) ta được \(y = - \left( {\frac{{ - \frac{7}{3}}}{3} + 1} \right) = - \left( { - \frac{7}{9} + 1} \right) = - \frac{2}{9}\), nên đường thẳng d2 không đi qua điểm \(\left( { - \frac{7}{3};2} \right)\).
Do đó phương án B là sai.
• Xét điểm \(\left( {0;\frac{1}{4}} \right)\)
Với x = 0, thay vào \(y = \frac{{1 - 3x}}{4}\) ta được \(y = \frac{1}{4}\), nên đường thẳng d1 đi qua điểm \(\left( {0;\frac{1}{4}} \right)\).
Với x = 0, thay vào \(y = - \left( {\frac{x}{3} + 1} \right)\) ta được y = –1, nên đường thẳng d2 không đi qua điểm \(\left( {0;\frac{1}{4}} \right)\).
Do đó phương án C là sai.
• Xét điểm (3; ‒2)
Với x = 3, thay vào \(y = \frac{{1 - 3x}}{4}\) ta được \(y = \frac{{1 - 3.3}}{4} = \frac{{1 - 9}}{4} = \frac{{ - 8}}{4} = - 2\), nên đường thẳng d1 đi qua điểm (3; ‒2).
Với x = 3, thay vào \(y = - \left( {\frac{x}{3} + 1} \right)\) ta được \(y = - \left( {\frac{3}{3} + 1} \right) = - 2\), nên đường thẳng d2 đi qua điểm (3; ‒2).
Do đó phương án D là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Do đường thẳng d: y = ax + b (a ≠ 0) song song với đường thẳng \(d':y = - 3x - \frac{2}{3}\) nên a = ‒3 (thoả mãn) và \(b \ne - \frac{2}{3}\).
Mà đường thẳng y = ax + b đi qua điểm A(‒2; ‒4) suy ra ‒4 = ‒3.(‒2) + b hay b = ‒10 (thoả mãn).
Do đó, đường thẳng cần tìm là y = ‒3x ‒ 10.
b) Đường thẳng d có hệ số góc bằng ‒3 nên y = ‒3x + b.
Với y = 0 vào y = 2x – 2 ta được 2x – 2 = 0, suy ra x = 1.
Do đó B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên B(1; 0).
Do đường thẳng d đi qua điểm B(1; 0) nên thay x = 1, y = 0 vào y = ‒3x + b ta có:
0 = ‒3.1 + b
Suy ra b = 3
Từ đó, ta tìm được d: y = –3x + 3.
Lời giải
Lời giải
a) Ta có: A(‒2; 0), B(0; 4).
b) Ta vẽ các điểm M, N lần lượt là trung điểm của OA, OB như hình vẽ:
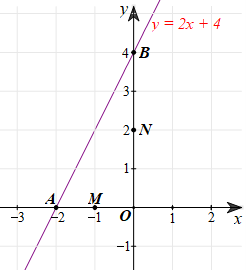
Từ đó ta có: M(‒1; 0), N(0; 2).
c) Do A, B lần lượt nằm trên Ox, Oy nên tam giác OAB vuông tại O.
Do đó diện tích của tam giác OAB là: \({S_{\Delta OAB}} = \frac{1}{2} \cdot OA \cdot OB\).
Mà M, N lần lượt là trung điểm của OA, OB nên \(OM = \frac{1}{2}OA,ON = \frac{1}{2}OB\).
Do M, N lần lượt nằm trên Ox, Oy nên tam giác OMN vuông tại O nên ta có diện tích của tam giác OMN bằng:
\({S_{\Delta OMN}} = \frac{1}{2} \cdot OM \cdot ON = \frac{1}{2} \cdot \frac{1}{2}OA \cdot \frac{1}{2}OB = \frac{1}{4} \cdot \frac{1}{2} \cdot OA.OB = \frac{1}{4}{S_{\Delta OAB}}\)
Vậy tỉ số phần trăm của diện tích tam giác \(OMN\) và diện tích tam giác \(OAB\) là:
\(\frac{{\frac{1}{4}{S_{\Delta OAB}}}}{{{S_{\Delta OAB}}}}.100\% = 25\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.