Câu hỏi:
12/07/2024 13,252
Trên đường tròn lượng giác lấy điểm M sao cho (OA, OM) = 40°. Gọi M' đối xứng với M qua gốc toạ độ. Khi đó số đo của góc lượng giác (OA, OM') bằng:
A. 40°+ k360°.
B. 140°+ k360°.
C. 220°+ k360°.
D. 50° + k360°.
Trên đường tròn lượng giác lấy điểm M sao cho (OA, OM) = 40°. Gọi M' đối xứng với M qua gốc toạ độ. Khi đó số đo của góc lượng giác (OA, OM') bằng:
A. 40°+ k360°.
B. 140°+ k360°.
C. 220°+ k360°.
D. 50° + k360°.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
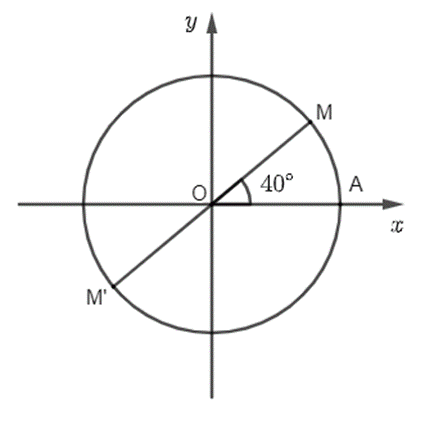
Vì M, M' đối xứng nhau qua gốc tọa độ O nên M, O, M' thẳng hàng.
Ta có:
(OA, OM') = (OA, OM) + (OM, OM') + k360° = 40° + 180° + k360° = 220° + k360°.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Vì \(\frac{\pi }{2} < \alpha < \pi \) nên tan α < 0.
Do đó, từ \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\), ta suy ra
\(\tan \alpha = - \sqrt {\frac{1}{{{{\cos }^2}\alpha }} - 1} = - \sqrt {\frac{1}{{{{\left( { - \frac{2}{5}} \right)}^2}}} - 1} = - \frac{{\sqrt {21} }}{2}\).
Lời giải
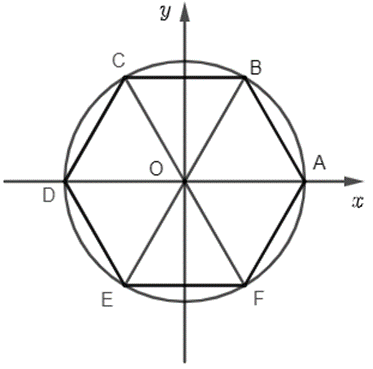
Vì ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \frac{{360^\circ }}{6} = 60^\circ = \frac{\pi }{3}\).
Khi đó, ta có:
\(\left( {OA,OB} \right) = \frac{\pi }{3} + k2\pi \);
\(\left( {OA,OC} \right) = \frac{\pi }{3} + \frac{\pi }{3} + k2\pi = \frac{{2\pi }}{3} + k2\pi \);
\(\left( {OA,OD} \right) = \pi + k2\pi \);
\(\left( {OA,OE} \right) = - \frac{\pi }{3} - \frac{\pi }{3} + k2\pi = - \frac{{2\pi }}{3} + k2\pi \);
\(\left( {OA,OF} \right) = - \frac{\pi }{3} + k2\pi \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
Bài tập Tổ hợp - Xác suất cơ bản, nâng cao có lời giải chi tiết (P6)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận