Giải SBT Toán 11 Cánh diều Góc lượng giác. Giá trị lượng giác của góc lượng giác có đáp án
54 người thi tuần này 4.6 1.4 K lượt thi 24 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
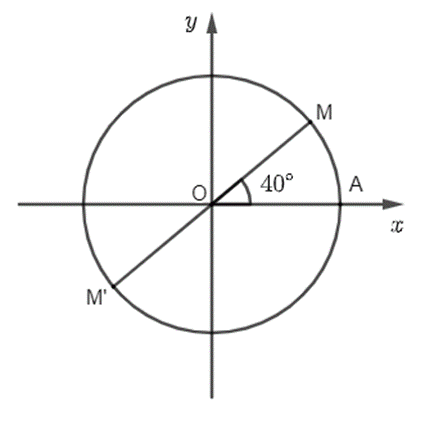
Vì M, M' đối xứng nhau qua gốc tọa độ O nên M, O, M' thẳng hàng.
Ta có:
(OA, OM') = (OA, OM) + (OM, OM') + k360° = 40° + 180° + k360° = 220° + k360°.
Lời giải
Đáp án đúng là: B
Vì \(\frac{\pi }{2} < \alpha < \pi \) nên tan α < 0.
Do đó, từ \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\), ta suy ra
\(\tan \alpha = - \sqrt {\frac{1}{{{{\cos }^2}\alpha }} - 1} = - \sqrt {\frac{1}{{{{\left( { - \frac{2}{5}} \right)}^2}}} - 1} = - \frac{{\sqrt {21} }}{2}\).
Lời giải
Đáp án đúng là: D
Ta có tan α + cot α = 2
Suy ra (tan α + cot α)2 = 22 = 4.
Mà (tan α + cot α)2 = tan2 α + 2tan α . cot α + cot2 α
= tan2 α + 2 . 1 + cot2 α = tan2 α + cot2 α + 2 = 4.
Do đó, tan2 α + cot2 α = 4 – 2 = 2.
Lời giải
Đáp án đúng là: A
\(A = \sin \left( {\pi + x} \right) + \cos \left( {\frac{\pi }{2} - x} \right) + \cot \left( {2\pi - x} \right) + \tan \left( {\frac{{3\pi }}{2} + x} \right)\)
\( = - \sin x + \sin x + \cot \left( {\pi + \pi - x} \right) + \tan \left( {\pi + \frac{\pi }{2} + x} \right)\)
\( = \cot \left( {\pi - x} \right) + \tan \left( {\frac{\pi }{2} + x} \right)\)
\( = \cot \left( { - x} \right) + \tan \left( {\pi + x - \frac{\pi }{2}} \right)\)
\( = - \cot x + \tan \left[ { - \left( {\frac{\pi }{2} - x} \right)} \right]\)
\( = - \cot x - \tan \left( {\frac{\pi }{2} - x} \right)\)
\( = - \cot x - \cot x = - 2\cot x\).
Lời giải
Đáp án đúng là: B
Vì tan α = 2 xác định nên cos α ≠ 0, hay cos2 α ≠ 0, do đó chia cả tử và mẫu của A cho cos2 α ta được:
\(A = \frac{{\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} - \frac{{2\sin \alpha .\cos \alpha }}{{{{\cos }^2}\alpha }}}}{{\frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{3{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}} = \frac{{{{\tan }^2}\alpha - 2\tan \alpha }}{{1 + 3{{\tan }^2}\alpha }} = \frac{{{2^2} - 2.2}}{{1 + {{3.2}^2}}} = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.