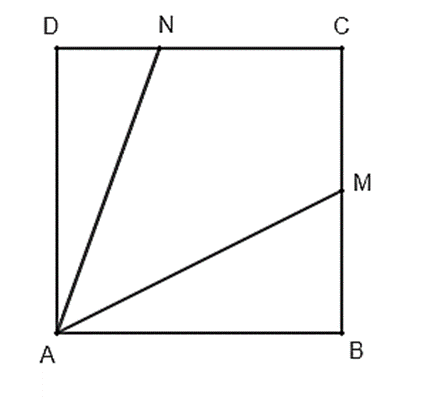
Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = \(\frac{1}{2}\)BC, DN = \(\frac{1}{3}\)DC (Hình 4).

Tính \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 11 Cánh Diều Các phép biến đổi lượng giác có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Trong tam giác vuông ABM, có \(\tan \widehat {BAM} = \frac{{BM}}{{BA}} = \frac{1}{2}\).

Trong tam giác vuông ADN, có \(\tan \widehat {DAN} = \frac{{DN}}{{AD}} = \frac{{DN}}{{DC}} = \frac{1}{3}\).

Do đó, \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\)\( = \frac{{\tan \widehat {BAM} + \tan \widehat {DAN}}}{{1 - \tan \widehat {BAM}.\tan \widehat {DAN}}}\)\( = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 - \frac{1}{2}.\frac{1}{3}}} = 1\).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chọn đẳng thức đúng trong các đẳng thức sau:

A. \({\sin ^4}x + {\cos ^4}x = \frac{{3 - \cos 4x}}{4}\).

B. \({\sin ^4}x + {\cos ^4}x = \frac{{3 + \cos 4x}}{4}\).

C. \({\sin ^4}x + {\cos ^4}x = \frac{{3 + \cos 4x}}{2}\).

D. \({\sin ^4}x + {\cos ^4}x = \frac{{3 - \cos 4x}}{2}\).

Xem đáp án

Lời giải

Đáp án đúng là: B

Ta có sin⁴ x + cos⁴ x = 1 – 2sin² x cos² x (theo Bài 9a)

= 1 – 2 (sin x cos x)² = \(1 - 2{\left( {\frac{{\sin 2x}}{2}} \right)^2} = 1 - 2.\frac{{{{\sin }^2}2x}}{4} = 1 - \frac{{2\left( {1 - {{\cos }^2}2x} \right)}}{4}\)

\( = 1 - \frac{{2 - 2{{\cos }^2}2x}}{4} = \frac{{4 - 2 + 2{{\cos }^2}2x}}{4}\)\( = \frac{{3 + \left( {2{{\cos }^2}2x - 1} \right)}}{4} = \frac{{3 + \cos 4x}}{4}\).

Vậy \({\sin ^4}x + {\cos ^4}x = \frac{{3 + \cos 4x}}{4}\).

Câu 2

Cho tam giác ABC, chứng minh rằng:

\(\tan \frac{A}{2}.\tan \frac{B}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{C}{2}.\tan \frac{A}{2} = 1\).

Xem đáp án

Lời giải

Ta có \(\frac{{A + B + C}}{2} = \frac{\pi }{2}\), suy ra \(\frac{A}{2} + \frac{B}{2} = \frac{\pi }{2} - \frac{C}{2}\) nên \(\tan \left( {\frac{A}{2} + \frac{B}{2}} \right) = \cot \frac{C}{2}\)

\( \Leftrightarrow \frac{{\tan \frac{A}{2} + \tan \frac{B}{2}}}{{1 - \tan \frac{A}{2}.\tan \frac{B}{2}}} = \frac{1}{{\tan \frac{C}{2}}}\)

\( \Leftrightarrow \left( {\tan \frac{A}{2} + \tan \frac{B}{2}} \right)\tan \frac{C}{2} = 1 - \tan \frac{A}{2}.\tan \frac{B}{2}\)

\( \Leftrightarrow \tan \frac{A}{2}.\tan \frac{C}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{A}{2}.\tan \frac{B}{2} = 1\)

\( \Leftrightarrow \tan \frac{A}{2}.\tan \frac{B}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{C}{2}.\tan \frac{A}{2} = 1\).

Câu 3