Một công ty dự định làm một đường ống dẫn từ một nhà máy ở địa điểm C trên bờ đến một địa điểm B trên biển. Khoảng cách giữa địa điểm A trên đảo với địa điểm B, địa điểm C lần lượt là 9 km, 15 km; AB vuông góc với BC (minh hoạ ở Hình 27).
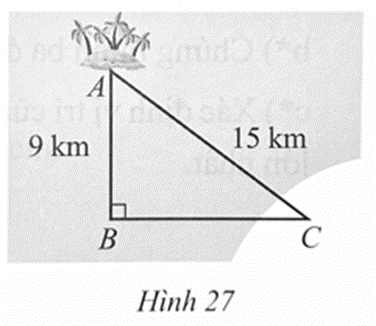
Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểm C đến địa điểm B là bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng (ngày 01/01/2023 theo nguồn https://www.google.com/finance/quote).
Một công ty dự định làm một đường ống dẫn từ một nhà máy ở địa điểm C trên bờ đến một địa điểm B trên biển. Khoảng cách giữa địa điểm A trên đảo với địa điểm B, địa điểm C lần lượt là 9 km, 15 km; AB vuông góc với BC (minh hoạ ở Hình 27).
Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểm C đến địa điểm B là bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng (ngày 01/01/2023 theo nguồn https://www.google.com/finance/quote).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng định lý Pythagore trong tam giác ABC vuông tại B, ta có:
AC2 = AB2 + BC2
Suy ra BC2 = AC2 ‒ BC2 = 152 ‒ 92 = 225 – 81 = 144.
Do đó \(BC = \sqrt {144} = 12\)(km).
Chi phí làm đường ống từ địa điểm \(C\) đến địa điểm \(B\) là:
5 000 . 23 635 . 12 = 1 418 100 000 (đồng).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
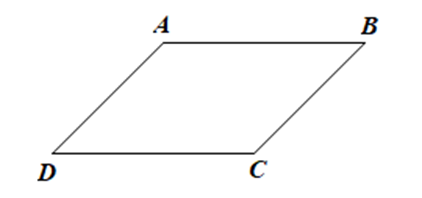
Do ABCD là hình bình hành nên \(\widehat A = \widehat C\), \(\widehat B = \widehat D\), \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Mà \(\widehat A = 3\widehat B\) nên \(\widehat A = \widehat C = 3\widehat B\)
Suy ra \(3\widehat B + \widehat B + 3\widehat B + \widehat B = 360^\circ \)
Do đó \(8\widehat B = 360^\circ \) nên \(\widehat B = 45^\circ \)
Vậy \(\widehat B = \widehat D = 45^\circ \), \(\widehat A = \widehat C = 3\widehat B = 3.45^\circ = 135^\circ \).
Lời giải
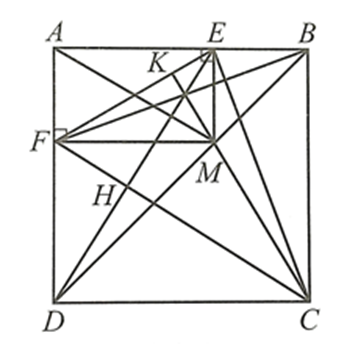
Gọi H là giao điểm của DE và CF, K là giao điểm của CM và EF.
Do ABCD là hình vuông nên ta có: \(\widehat {DAB} = 90^\circ ,CD = DA,\widehat {ADB} = \widehat {ABD} = \widehat {DBC} = 45^\circ \)
Tương tự câu \({\rm{a}}\), ta chứng minh được BF ⊥ CE.
Xét ∆ABM và ∆CBM có:
AB = BC, \(\widehat {ABM} = \widehat {CBM}\left( { = 45^\circ } \right)\), cạnh BM chung
Do đó ∆ABM = ∆CBM (c.g.c)
Suy ra AM = CM (hai cạnh tương ứng)
Mà EF = AM (vì AEMF là hình chữ nhật), suy ra EF = CM.
Xét ∆DEF và ∆FCM có:
DE = FC, EF = CM, DF = FM
Do đó ∆DEF = ∆FCM (c.c.c)
Suy ra \(\widehat {DEF} = \widehat {FCM}{\rm{\;}}\) (hai góc tương ứng)
Hay \(\widehat {FEH} = \widehat {FCK}\).
Trong tam giác HEF vuông tại H, ta có \(\widehat {FEH} + \widehat {EFH} = 90^\circ \).
Suy ra \(\widehat {FCK} + \widehat {EFH} = 90^\circ \) hay \(\widehat {FCK} + \widehat {KFC} = 90^\circ \).
Do đó \(\widehat {CKF} = 90^\circ \). Do đó CK ⊥ EF.
Trong tam giác CEF, ta có: EH ⊥ CF, FB ⊥ CE, CM ⊥ EF nên ba đường thẳng EH, FB, CM là các đường cao của tam giác CEF.
Hay ba đường thẳng DE, BF, CM là các đường cao của tam giác CEF.
Vậy ba đường thẳng DE, BF, CM cùng đi qua một điểm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo