Cho hình bình hành ABCD có BC = 2AB. Gọi M, N lần lượt là trung điểm của BC, AD.
Gọi P là giao điểm của AM và BN, Q là giao điểm của CN và DM. Chứng minh tứ giác PMQN là hình chữ nhật.
Cho hình bình hành ABCD có BC = 2AB. Gọi M, N lần lượt là trung điểm của BC, AD.
Gọi P là giao điểm của AM và BN, Q là giao điểm của CN và DM. Chứng minh tứ giác PMQN là hình chữ nhật.
Câu hỏi trong đề: Giải SBT Toán 8 Cánh Diều Bài tập cuối chương 5 có đáp án !!
Quảng cáo
Trả lời:
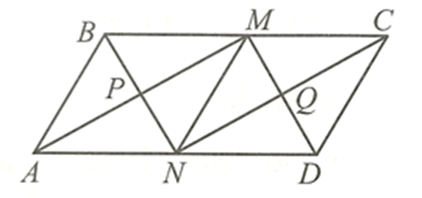
Tương tự câu a, ta chứng minh được MANC là hình bình hành.
Do MBND, MANC đều là hình bình hành nên PN // MQ, PM // NQ (do P là giao điểm của AM và BN, Q là giao điểm của CN và DM).
Suy ra tứ giác PMQN là hình bình hành.
Xét ∆ABN và ∆MNB có:
AN = BM, \[\widehat {ANB} = \widehat {MBN}\](hai góc so le trong do BM // AN), cạnh BN chung
Do đó ∆ABN = ∆MNB (c.g.c). Suy ra AB = MN (hai cạnh tương ứng0
Tứ giác ABMN có AB = BM = MN = AN nên ABMN là hình thoi.
Suy ra AM ⊥ BN, do đó \(\widehat {MPN} = 90^\circ \).
Hình bình hành PMQN có \(\widehat {MPN} = 90^\circ \) nên PMQN là hình chữ nhật.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
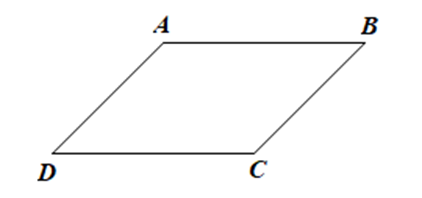
Do ABCD là hình bình hành nên \(\widehat A = \widehat C\), \(\widehat B = \widehat D\), \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Mà \(\widehat A = 3\widehat B\) nên \(\widehat A = \widehat C = 3\widehat B\)
Suy ra \(3\widehat B + \widehat B + 3\widehat B + \widehat B = 360^\circ \)
Do đó \(8\widehat B = 360^\circ \) nên \(\widehat B = 45^\circ \)
Vậy \(\widehat B = \widehat D = 45^\circ \), \(\widehat A = \widehat C = 3\widehat B = 3.45^\circ = 135^\circ \).
Câu 2
Một công ty dự định làm một đường ống dẫn từ một nhà máy ở địa điểm C trên bờ đến một địa điểm B trên biển. Khoảng cách giữa địa điểm A trên đảo với địa điểm B, địa điểm C lần lượt là 9 km, 15 km; AB vuông góc với BC (minh hoạ ở Hình 27).
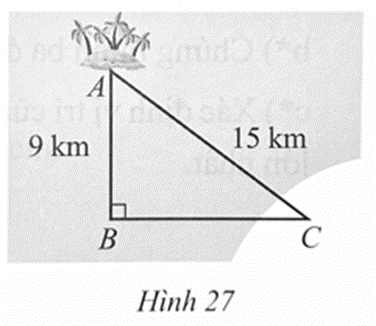
Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểm C đến địa điểm B là bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng (ngày 01/01/2023 theo nguồn https://www.google.com/finance/quote).
Một công ty dự định làm một đường ống dẫn từ một nhà máy ở địa điểm C trên bờ đến một địa điểm B trên biển. Khoảng cách giữa địa điểm A trên đảo với địa điểm B, địa điểm C lần lượt là 9 km, 15 km; AB vuông góc với BC (minh hoạ ở Hình 27).

Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểm C đến địa điểm B là bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng (ngày 01/01/2023 theo nguồn https://www.google.com/finance/quote).
Lời giải
Áp dụng định lý Pythagore trong tam giác ABC vuông tại B, ta có:
AC2 = AB2 + BC2
Suy ra BC2 = AC2 ‒ BC2 = 152 ‒ 92 = 225 – 81 = 144.
Do đó \(BC = \sqrt {144} = 12\)(km).
Chi phí làm đường ống từ địa điểm \(C\) đến địa điểm \(B\) là:
5 000 . 23 635 . 12 = 1 418 100 000 (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.