Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Quảng cáo
Trả lời:
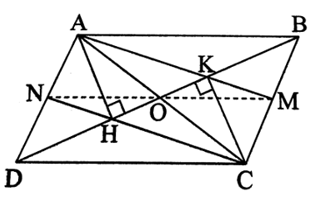
a) Do ABCD là hình bình hành nên AB // CD
Suy ra (hai góc so le trong) hay .
Xét ∆AHB vuông tại H và ∆CKD vuông tại K, ta có:
AB = CD (do ABCD là hình bình hành); (chứng minh trên).
Suy ra ∆AHB = ∆CKD (cạnh huyền – góc nhọn)
Do đó AH = CK (hai cạnh tương ứng)
Ta có: AH ⊥ BD, CK ⊥ BD suy ra AH // CK.
Tứ giác AHCK có: AH // CK, AH = CK nên là hình bình hành.
b) Vì AHCK là hình bình hành nên AK // CH, hay AM // CN. (1)
Hơn nữa, ABCD là hình bình hành và N ∈ AD, M ∈ BC nên AN // CM. (2)
Từ (1) và (2) suy ra ANCM là hình bình hành.
Vậy AN = CM.
c) Tứ giác AHCK là hình bình hành có hai đường chéo AC, HK cắt nhau tại trung điểm
O của HK nên O cũng là trung điểm của AC.
Tứ giác ANCM là hình bình hành có hai đường chéo AC, NM cắt nhau tại trung điểm
O của AC nên O cũng là trung điểm của MN.
Vậy M, O, N thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
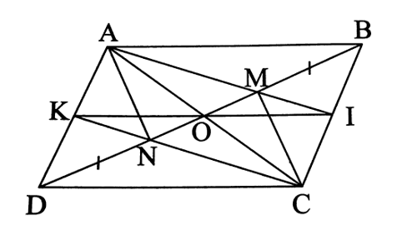
a) Vì ABCD là hình bình hành nên AB = CD và AB // CD.
Suy ra (hai góc so le trong).
Xét ∆AMB và ∆CND, ta có:
AB = CD (chứng minh trên);
(chứng minh trên);
BM = DN (giả thiết).
Suy ra ∆AMB = ∆CND (c.g.c).
b) Ta có ∆AMB = ∆CND (theo câu a), suy ra AM = CN (1)
Ta có: BM + MN = BN và DN + MN = DM; mà BM = DN, suy ra BN = DM.
Xét ∆ABN và ∆CDM, ta có:
AB = CD (chứng minh trên);
BN = DM (chứng minh trên)
Suy ra ∆ABN = ∆CDM (c.g.c), suy ra AN = CM (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
c) Vì AMCN là hình bình hành nên OA = OC.
∆ABC có OA = OC, suy ra BO là đường trung tuyến của ∆ABC.
ABCD là hình bình hành nên khi O là trung điểm của đường chéo AC thì O cũng là trung điểm của đường chéo BD, khi đó
Ta lại có: , suy ra
Do đó M là trọng tâm ∆ABC.
Khi đó Suy ra AM = 2MI.
d) Vì AMCN là hình bình hành nên AM // CN, mà M ∈ AI, N ∈ CK, nên AI // CK. (3)
Hơn nữa, AD // BC, K ∈ AD, I ∈ BC, nên AK // CI (4)
Từ (3), (4) suy ra AKCI là hình bình hành.
Mà O là trung điểm của AC, suy ra O cũng là trung điểm của KI hay I và K đối xứng nhau qua O.
Lời giải

Tứ giác ABCD là hình bình hành nên OA = OC và OB = OD.
Ta có: (N là trung điểm của OD); (M là trung điểm của OB); OB = OD (chứng minh trên).
Suy ra OM = ON.
Xét tứ giác AMCN ta có: OM = ON, OA = OC (chứng minh trên)
Do đó, tứ giác AMCN là hình bình hành.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.