Một người đo chiều cao của một cái cây bằng cách chôn một chiếc cọc xuống đất, cọc cao 2,4 m và cách vị trí gốc cây 19 m. Người đo đứng cách xa chiếc cọc 1 m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6 m (H.9.49).
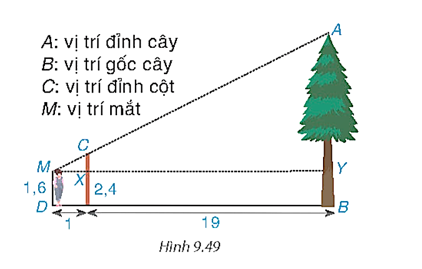
Một người đo chiều cao của một cái cây bằng cách chôn một chiếc cọc xuống đất, cọc cao 2,4 m và cách vị trí gốc cây 19 m. Người đo đứng cách xa chiếc cọc 1 m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6 m (H.9.49).

Quảng cáo
Trả lời:
Ta có CX = 2,4 – 1,6 = 0,8 (m).
MY = 1 + 19 = 20 (m).
Xét tam giác MXC và tam giác MYA có:
chung
Do đó: ∆MXC ∽ ∆MYA (g.g).
Suy ra . Do đó, (m).
Vậy chiều cao của cây là AB = AY + YB = AY + MD = 16 + 1,6 = 17,6 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
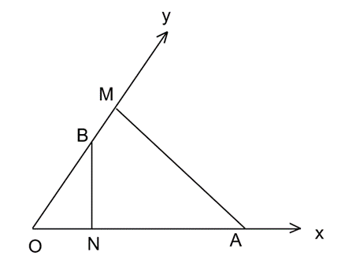
Xét hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có:
Góc nhọn chung.
Suy ra ΔOAM ∽ ΔOBN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.