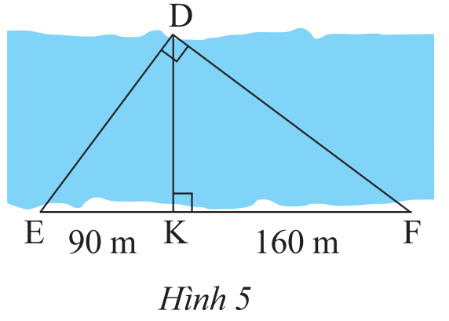
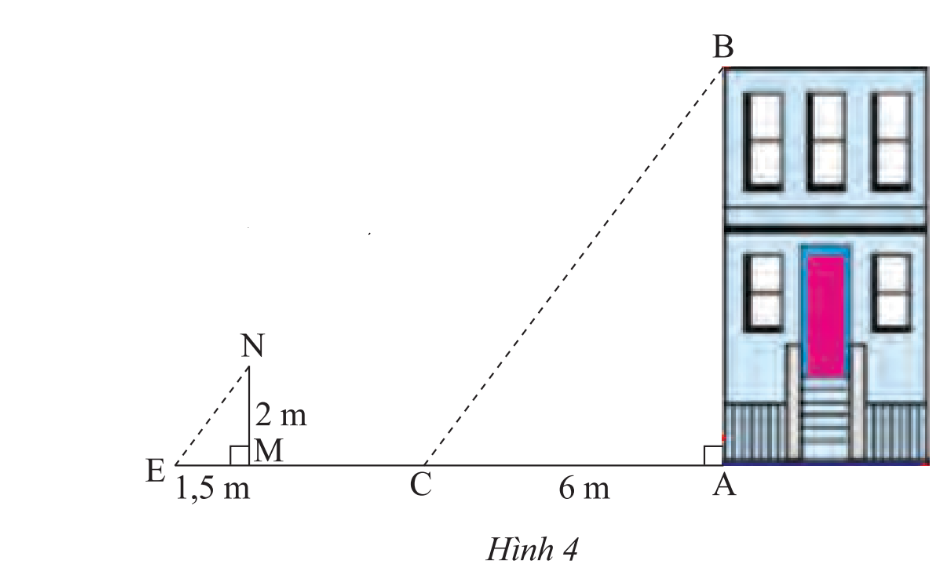
Bóng của một căn nhà trên mặt đất có độ dài 6m. Cùng thời điểm đó, một cọc sắt cao 2m cắm vuông góc với mặt đất có bóng dài 1,5 m (Hình 4). Tính chiều cao ngôi nhà.

Lời giải:

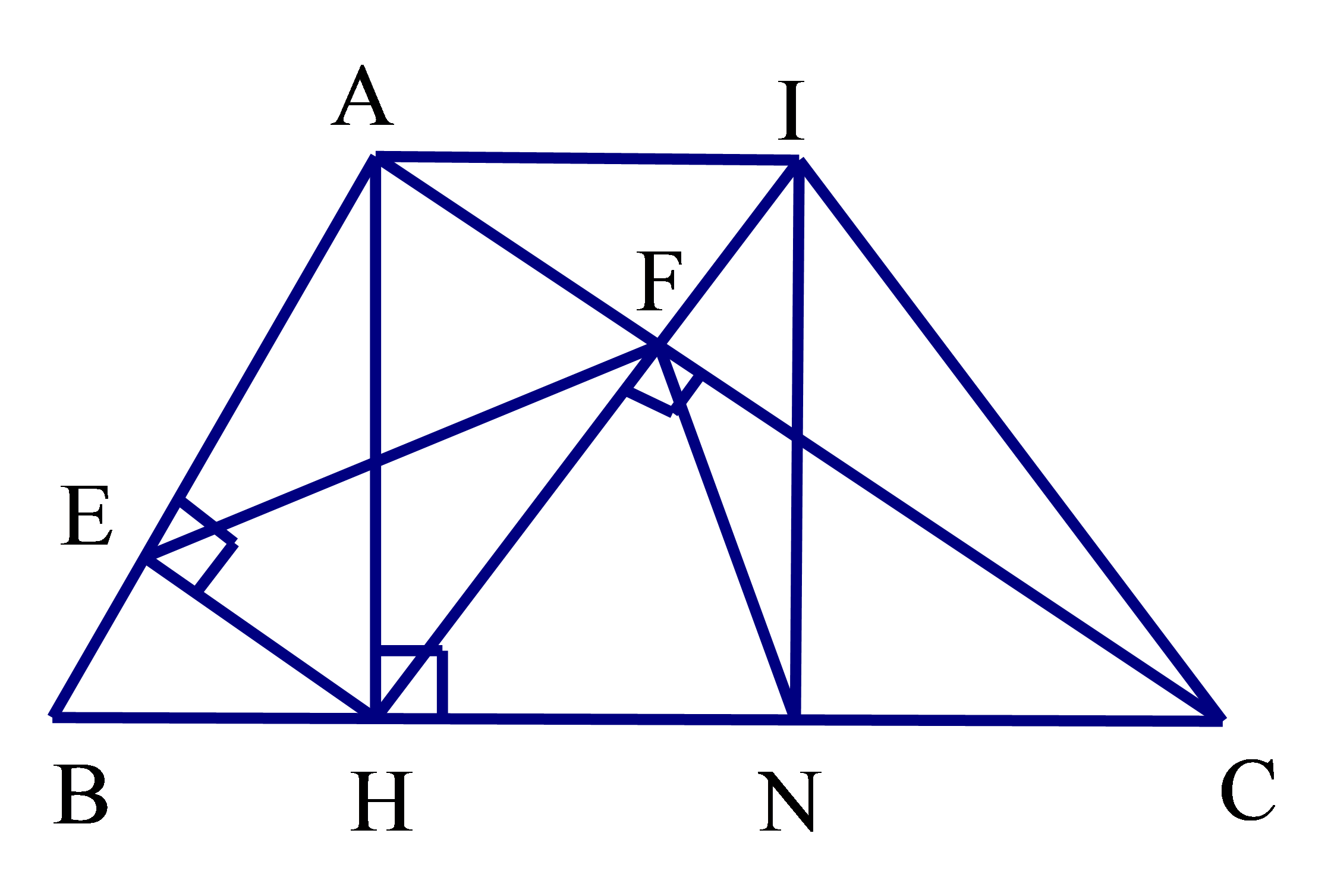
a) Xét tam giác vuông ABH và CBA ta có:

\[\widehat B\] chung

Suy ra ΔABH ᔕ ΔCBA nên \[\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\;\] hay AB² = BH.BC

b) c) Tứ giác AEHF có 4 góc vuông suy ra AEHF là hình chữ nhật 

Do đó \[\widehat {AEF} = \widehat {AEH}\]

ΔABH ᔕ ΔCBA nên \[\widehat {EAH} = \widehat {ACB}\]

Xét tam giác AEF và ACB ta có:

\[\widehat A\] chung

\[\widehat {EAH} = \widehat {ACB}\]

Suy ra ΔAEF ᔕ ΔACB (g.g) nên \[\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\;\] hay AE.AB = AF.AC

d) Xét tam giác vuông HNI và HFC ta có:

\[\widehat H\] chung

Suy ra ΔHNI ᔕ ΔHFC (g.g)

Nên \[\frac{{HN}}{{HF}} = \frac{{HI}}{{HC}}\;\] hay \[\frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}\]

Xét tam giác HNF và HIC ta có:

\[\widehat H\] chung

\[\frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}\]

Lời giải:

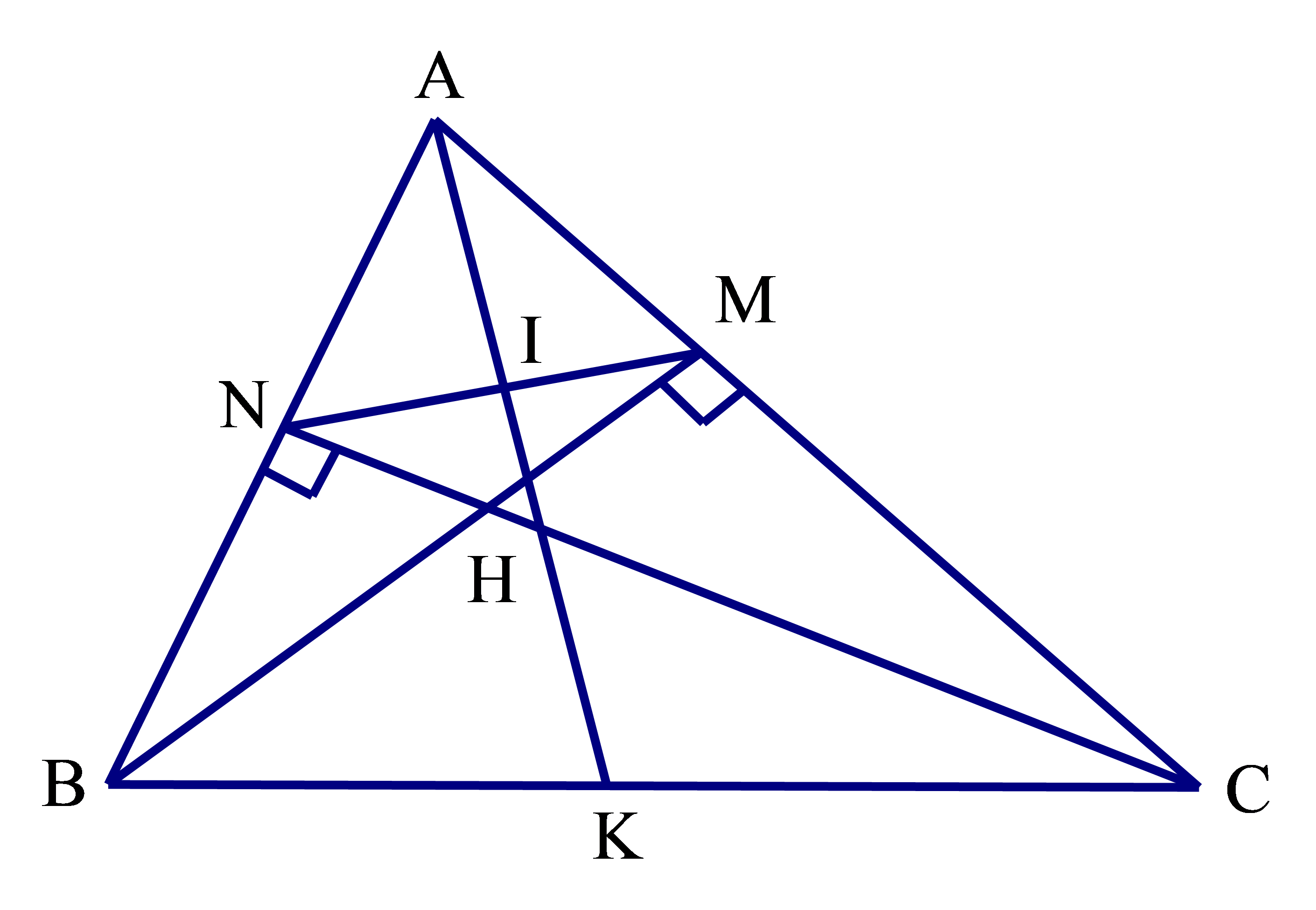
a) Xét tam giác vuông ABM và ACN có:

\[\widehat A\] chung

Suy ra ΔABM ᔕ ΔACN (g.g)

Nên \[\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\;\] hay \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\]

Xét tam giác AMN và ABC ta có:

\[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\]

\[\widehat A\] chung

Suy ra ΔAMN ᔕ ΔABC (c.g.c).

b) ΔAMN ᔕ ΔABC, AK là phân giác của \[\widehat {BAC}\] 

Suy ra \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{AI}}{{AK}}\]

Xét tam giác AIM và AKB ta có:

\[\frac{{AM}}{{AB}} = \frac{{AI}}{{AK}}\]

\[\widehat {IAM} = \widehat {IAN}\] (vì AK là phân giác \[\widehat {BAC}\])

Suy ra ΔAIM ᔕ ΔAKB nên \[\frac{{IM}}{{KB}} = \frac{{AI}}{{AK}}\;\] (1)

Xét tam giác AIN và AKC ta có:

\[\frac{{AN}}{{AC}} = \frac{{AI}}{{AK}}\]

\[\widehat {IAM} = \widehat {IAN}\] (vì AK là phân giác \[\widehat {BAC}\])

Suy ra ΔAIN ᔕ ΔAKC nên \[\frac{{IN}}{{KC}} = \frac{{AI}}{{AK}}\;\] (2)

Từ (1) và (2) suy ra \[\frac{{IM}}{{KB}} = \frac{{IN}}{{KC}}\;\] hay \[\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\].