Câu hỏi:
13/07/2024 17,536
Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H.
a) Chứng minh rằng ΔAMN ᔕ ΔABC.
b) Phân giác của \[\widehat {BAC}\] cắt MN và BC lần lượt tại I và K. Chứng minh rằng \[\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\].
Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H.
a) Chứng minh rằng ΔAMN ᔕ ΔABC.
b) Phân giác của \[\widehat {BAC}\] cắt MN và BC lần lượt tại I và K. Chứng minh rằng \[\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\].
Câu hỏi trong đề: Giải SGK Toán 8 CTST Bài tập cuối chương 8 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
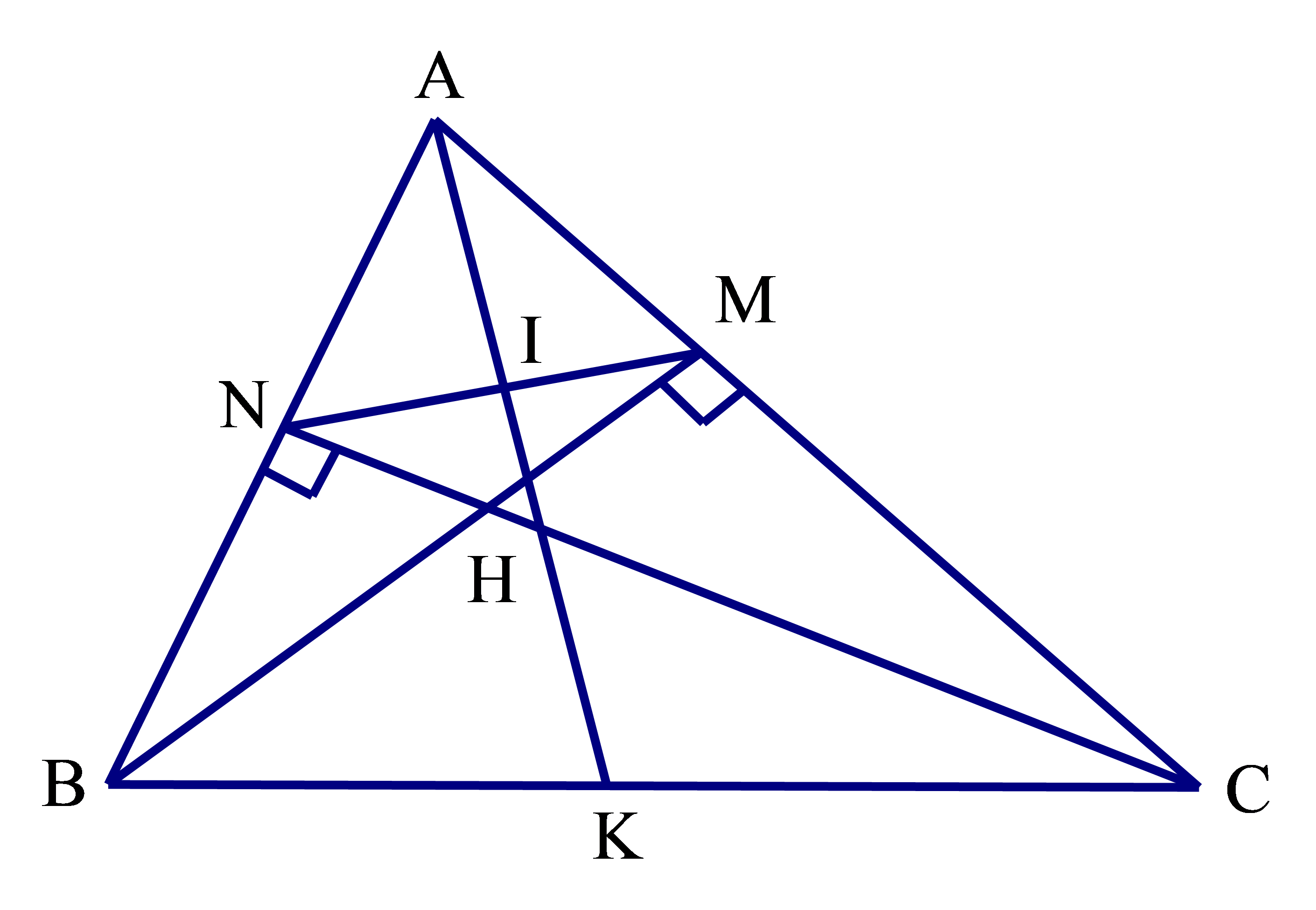
a) Xét tam giác vuông ABM và ACN có:
\[\widehat A\] chung
Suy ra ΔABM ᔕ ΔACN (g.g)
Nên \[\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\;\] hay \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\]
Xét tam giác AMN và ABC ta có:
\[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\]
\[\widehat A\] chung
Suy ra ΔAMN ᔕ ΔABC (c.g.c).
b) ΔAMN ᔕ ΔABC, AK là phân giác của \[\widehat {BAC}\]
Suy ra \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{AI}}{{AK}}\]
Xét tam giác AIM và AKB ta có:
\[\frac{{AM}}{{AB}} = \frac{{AI}}{{AK}}\]
\[\widehat {IAM} = \widehat {IAN}\] (vì AK là phân giác \[\widehat {BAC}\])
Suy ra ΔAIM ᔕ ΔAKB nên \[\frac{{IM}}{{KB}} = \frac{{AI}}{{AK}}\;\] (1)
Xét tam giác AIN và AKC ta có:
\[\frac{{AN}}{{AC}} = \frac{{AI}}{{AK}}\]
\[\widehat {IAM} = \widehat {IAN}\] (vì AK là phân giác \[\widehat {BAC}\])
Suy ra ΔAIN ᔕ ΔAKC nên \[\frac{{IN}}{{KC}} = \frac{{AI}}{{AK}}\;\] (2)
Từ (1) và (2) suy ra \[\frac{{IM}}{{KB}} = \frac{{IN}}{{KC}}\;\] hay \[\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
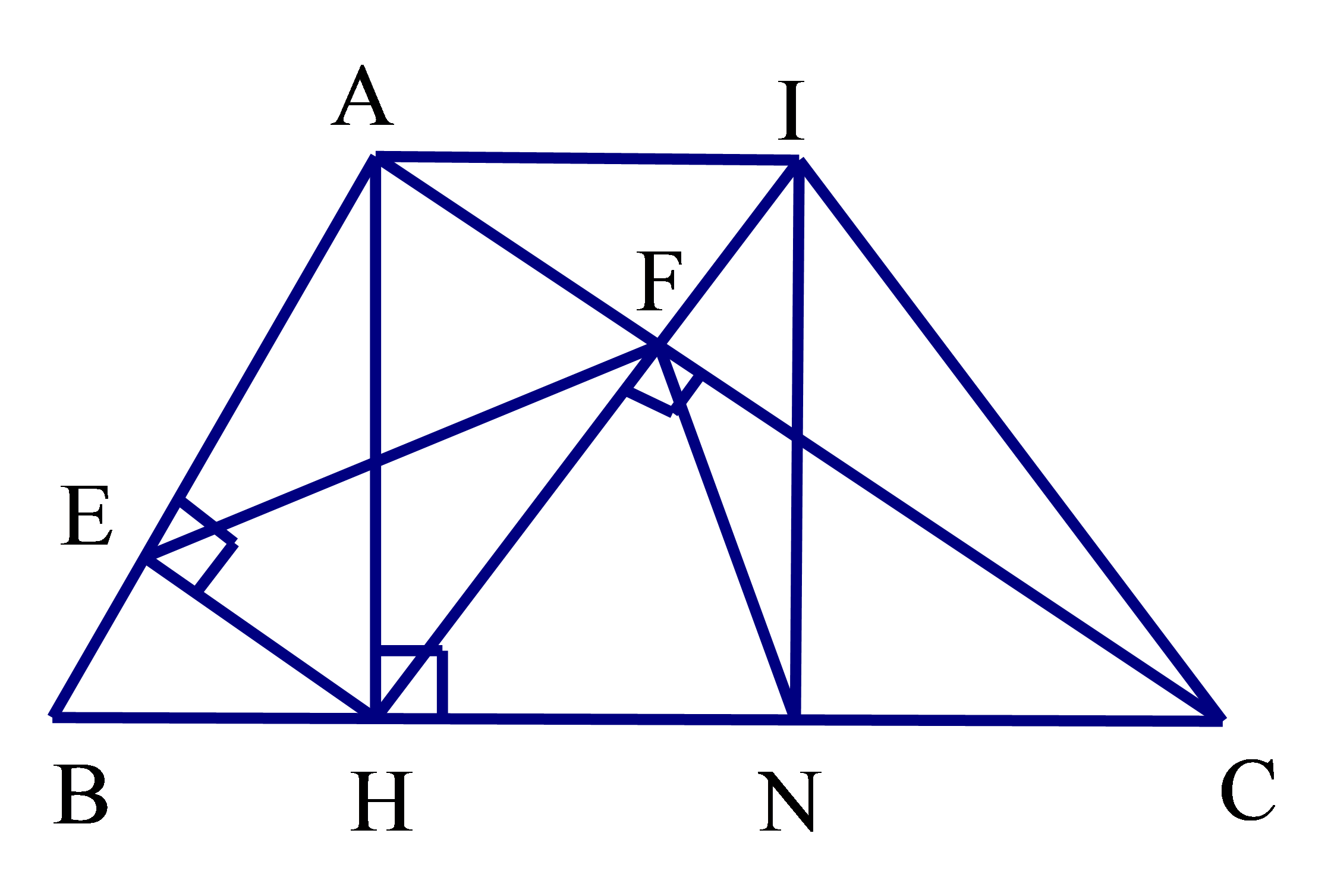
a) Xét tam giác vuông ABH và CBA ta có:
\[\widehat B\] chung
Suy ra ΔABH ᔕ ΔCBA nên \[\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\;\] hay AB2 = BH.BC
b) c) Tứ giác AEHF có 4 góc vuông suy ra AEHF là hình chữ nhật
Do đó \[\widehat {AEF} = \widehat {AEH}\]
ΔABH ᔕ ΔCBA nên \[\widehat {EAH} = \widehat {ACB}\]
Xét tam giác AEF và ACB ta có:
\[\widehat A\] chung
\[\widehat {EAH} = \widehat {ACB}\]
Suy ra ΔAEF ᔕ ΔACB (g.g) nên \[\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\;\] hay AE.AB = AF.AC
d) Xét tam giác vuông HNI và HFC ta có:
\[\widehat H\] chung
Suy ra ΔHNI ᔕ ΔHFC (g.g)
Nên \[\frac{{HN}}{{HF}} = \frac{{HI}}{{HC}}\;\] hay \[\frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}\]
Xét tam giác HNF và HIC ta có:
\[\widehat H\] chung
\[\frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}\]
Suy ra ΔHNF ᔕ ΔHIC (c.g.c).
Lời giải
Lời giải:
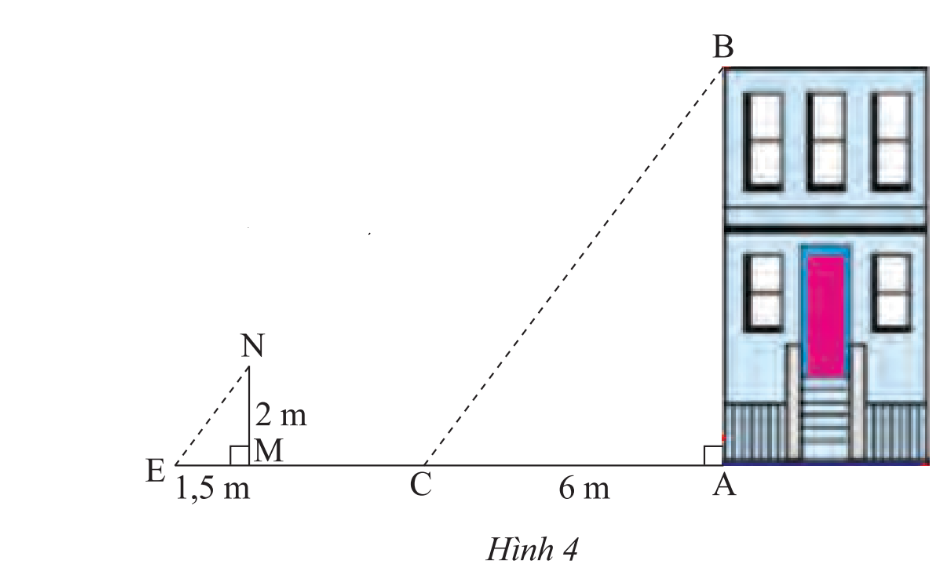
Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau nên\[\widehat C = \widehat E\].
Xét hai tam giác vuông ABC và tam giác MNE có: \[\widehat C = \widehat E\]
Do đó ΔABC ᔕ ΔMNE (g.g)
Suy ra: \[\frac{{AC}}{{ME}} = \frac{{AB}}{{MN}}\]
Thay số: \[\frac{6}{{1,5}} = \frac{{AB}}{{2\;}}\] suy ra AB = 8 (m)
Vậy chiều cao ngôi nhà là 8 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận