Câu hỏi:
13/07/2024 315
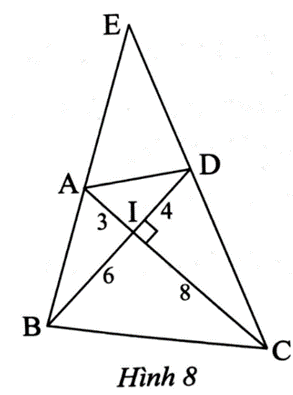
Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC ⊥ BD, chứng minh rằng:
∆AIB ᔕ ∆DIC.
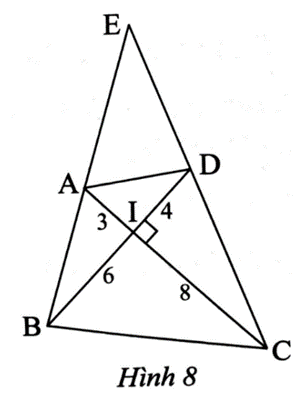
Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC ⊥ BD, chứng minh rằng:
∆AIB ᔕ ∆DIC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \[\frac{{IA}}{{ID}} = \frac{3}{4}\]; \[\frac{{IB}}{{IC}} = \frac{6}{8} = \frac{3}{4}\] suy ra \[\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\].
Xét ∆AIB vuông tại I và ∆DIC vuông tại I có \[\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\].
Suy ra ∆AIB ᔕ ∆DIC
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
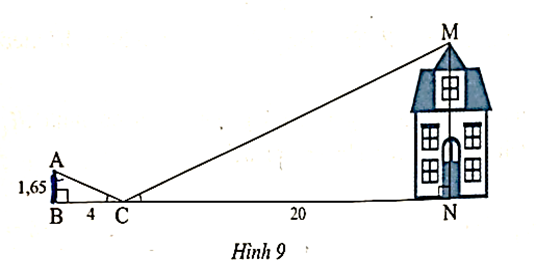
Xét ∆ABC vuông tại B và ∆MNC vuông tại N có \[\widehat {ACB} = \widehat {MCN}\].
Do đó ∆ABC ᔕ ∆MNC (g.g).
Suy ra \[\frac{{AB}}{{MN}} = \frac{{BC}}{{NC}}\] hay \[\frac{{1,65}}{{MN}} = \frac{4}{{20}}\].
Do đó \[MN = \frac{{1,65\,.\,20}}{4} = 8,25\] (m).
Vậy chiều cao MN của căn nhà là 8,25 m.
Lời giải
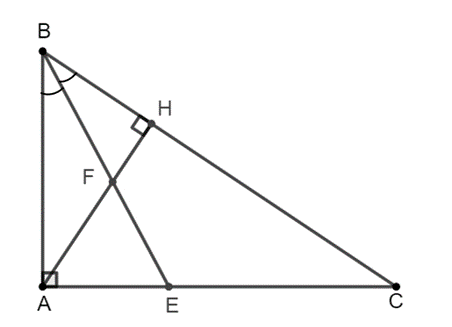
Xét ∆ABC có BE là tia phân giác của \[\widehat B\], suy ra \[\frac{{AB}}{{BC}} = \frac{{AE}}{{EC}}\] (1)
Xét ∆ABH có BF là tia phân giác của \[\widehat B\], suy ra \[\frac{{FH}}{{AF}} = \frac{{BH}}{{AB}}\] (2)
Xét ∆ABH vuông tại H và ∆ABC vuông tại A có \[\widehat B\] chung.
Do đó ∆ABH ᔕ ∆CBA, suy ra \[\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\] (3)
Từ (1); (2) và (3) suy ra \[\frac{{AE}}{{EC}} = \frac{{FH}}{{AF}}\].
Do đó AE . AF = EC . FH.
Mà AE = AF, suy ra AE2 = EC . FH (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo