Cho ∆ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của \[\widehat {BAC}\] cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A cắt BC tại E. Tính độ dài DB, DC, EB.
Cho ∆ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của \[\widehat {BAC}\] cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A cắt BC tại E. Tính độ dài DB, DC, EB.
Quảng cáo
Trả lời:
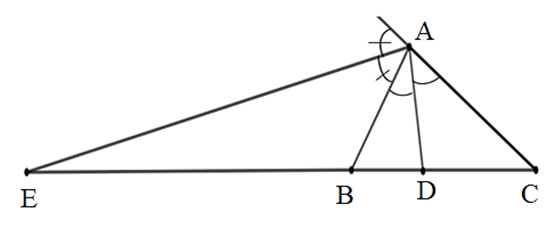
• Vì AD là phân giác của \[\widehat {BAC}\] trong ∆ABC nên ta có
\[\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\]\[ = \frac{6}{9} = \frac{2}{3}\].
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\[\frac{{DB}}{2} = \frac{{DC}}{3} = \frac{{DB + DC}}{{2 + 3}} = \frac{{BC}}{5} = \frac{{10}}{5} = 2\].
Suy ra \[\frac{{DB}}{2} = 2\]và \[\frac{{DC}}{3} = 2\].
Do đó DB = 4 cm; DC = 6 cm.
• Vì AE là phân giác ngoài tại đỉnh A của ∆ABC nên ta có
\[\frac{{EB}}{{EC}} = \frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3}\].
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\[\frac{{EC}}{3} = \frac{{EB}}{2} = \frac{{EC - EB}}{{3 - 2}} = \frac{{BC}}{1} = 10\].
Do đó \[\frac{{EB}}{2} = 10\] suy ra EB = 20 cm.
Vậy DB = 4 cm, DC = 6 cm, EB = 20 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
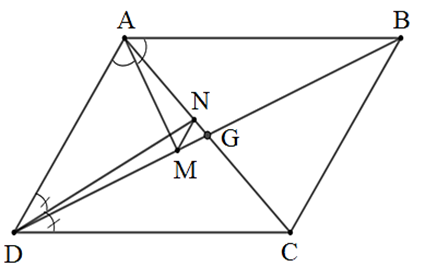
Gọi G là giao điểm của AC và BD.
• Vì DN là phân giác của \[\widehat {ADC}\] trong ∆ADC nên \[\frac{{NA}}{{NC}} = \frac{{AD}}{{DC}}\].
• Vì AM là phân giác của \[\widehat {BAD}\] trong ∆ABD nên \[\frac{{MD}}{{MB}} = \frac{{AD}}{{AB}}\]= \[\frac{{AD}}{{DC}}\] (vì AB = DC).
Suy ra \[\frac{{MD}}{{MB}} = \frac{{NA}}{{NC}}\].
Do đó \[\frac{{NA}}{{MD}} = \frac{{NC}}{{MB}} = \frac{{NA + NC}}{{MD + MB}} = \frac{{AC}}{{BD}} = \frac{{AG}}{{DG}}\] (AC = 2AG; BD = 2BG)
Khi đó \[\frac{{NA}}{{AG}} = \frac{{MD}}{{DG}}\].
Xét ∆AGD có \[\frac{{NA}}{{AG}} = \frac{{MD}}{{DG}}\]nên theo định lí Thalès đảo, ta có MN // AD.
Lời giải
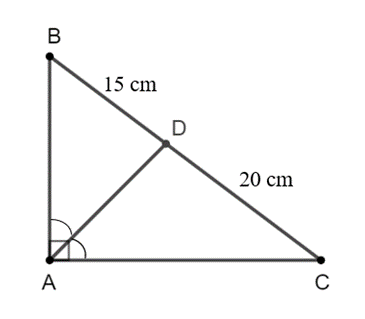
Ta có AD là phân giác của \[\widehat {BAC}\] trong ∆ABC, suy ra \[\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\].
Suy ra \[\frac{{15}}{{20}} = \frac{{AB}}{{AC}}\] hay \[\frac{{AB}}{{15}} = \frac{{AC}}{{20}}\].
Suy ra \[\frac{{A{B^2}}}{{225}} = \frac{{A{C^2}}}{{400}} = \frac{{A{B^2} + A{C^2}}}{{225 + 400}} = \frac{{B{C^2}}}{{625}}\] (áp dụng định lí Pythagore trong ∆ABC vuông).
Ta có BC = BD + DC = 15 + 20 = 35 (cm).
Nên \[\frac{{A{B^2}}}{{225}} = \frac{{A{C^2}}}{{400}} = \frac{{{{35}^2}}}{{625}} = \frac{{49}}{{25}}\].
Suy ra AB2 \[ = \frac{{49.225}}{{25}}\] = 441 và AC2\[ = \frac{{49.400}}{{25}}\] = 784.
Vậy AB = 21 cm; AC = 28 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.