Câu hỏi:

13/07/2024 4,542

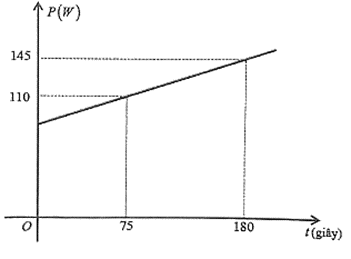
Chị Lan đun sôi nước bằng ấm điện. Biết rằng mối liên hệ giữa công suất hao phí P(W) của ấm điện và thời gian đun t (giây) được mô hình hóa bởi một hàm số bậc nhất có dạng P = at + b và có đồ thị như hình bên.

a) Hãy xác định các hệ số a và b.
b) Nếu đun nước với công suất hao phí là 105 (W) thì thời gian đun là bao lâu?

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 6) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Quan sát đồ thị ta thấy:

Tại thời điểm t = 75 (giây) thì công suất hao phí là 110W nên đồ thị hàm số P = at + b đi qua điểm (75;110). Ta có phương trình: 110 = 75a + b. (1)

Tại thời điểm t = 180 (giây) thì công suất hao phí là 145W nên đồ thị hàm số P = at + b đi qua điểm (180;145). Ta có phương trình: 145 = 180a + b. (2)

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} 110 = 75 a + b \\ 145 = 180 a + b \end{cases}$

$\{\begin{cases} 75 a + b = 110 \\ 105 a = 35 \end{cases} \Leftrightarrow \{\begin{cases} b = 110 - 75. \frac{1}{3} \\ a = \frac{1}{3} \end{cases} \Leftrightarrow \{\begin{cases} b = 85 \\ a = \frac{1}{3} \end{cases}$ .

Vậy các hệ số cần tìm là $a = \frac{1}{3}, b = 85$ .

b) Từ câu a) ta có: $P = \frac{1}{3} t + 85$ . Gọi t₀ (giây) là thời gian đun nước với công suất hao phí là $P (t_{0}) = 105 W$ , ta có phương trình

$\frac{1}{3} t_{0} + 85 = 105 \Leftrightarrow t_{0} = 60$

Vậy thời gian để đun nước với công suất hao phí 105 (W) là 60 giây.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC nhọn (AB < AC) có đường cao AH và nội tiếp đường tròn (O). Gọi E, F lần lượt là hình chiếu của H lên các cạnh AB, AC. Đường kính AD của (O) cắt EF tại K và DH cắt (O) tại L (L khác D).

a) Chứng minh các tứ giác AEHF và ALHF nội tiếp.

b) Chứng minh tứ giác BÈC nội tiếp và AD vuông góc với EF tại K.

c) Tia FE cắt (O) tại P và cắt BC tại M. Chứng minh AP = AH và ba điểm A, L, M thẳng hàng.

Xem đáp án

Lời giải

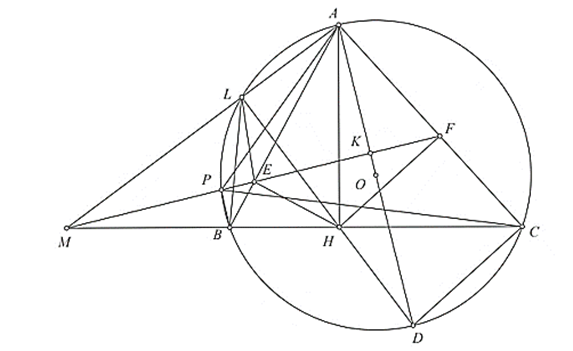
Cho tam giác ABC nhọn (AB < AC) có đường cao AH và nội tiếp đường tròn (O). Gọi E, F lần lượt là hình chiếu của H lên các cạnh AB, AC. (ảnh 1)

a) Ta có: $H E ⊥ A B, H F ⊥ A C$ nên $\hat{A E H} = \hat{A F H} = 90 °$ .

Tứ giác AEHF có $\hat{A E H}, \hat{A F H}$ là hai góc đối và $\hat{A E H} + \hat{A F H} = 90 ° + 90 ° = 180 °$ nên tứ giác AEHF nội tiếp.

Do AD là đường kính của đường tròn (O) nên $\hat{A L D} = 90 °$ (góc nội tiếp chắn nửa đường tròn).

Tứ giác ALHF có $\hat{A L H}, \hat{A F H}$ là hai góc đối và $\hat{A L H} + \hat{A F H} = 90 ° + 90 ° = 180 °$ nên tứ giác ALHF nội tiếp.

b) Ta có: $A H ⊥ B C$ và $H E ⊥ A B$ nên $\hat{E B H} = 90 ° - \hat{B H E} = \hat{A H E}$ .

Mà $\hat{A H E} = \hat{A F E}$ (do tứ giác AEHF nội tiếp).

Suy ra $\hat{A F E} = \hat{E B C}$ (1).

Tứ giác BEFC có góc ngoài tại đỉnh F bằng góc trong tại đỉnh B nên tứ giác BEFC nội tiếp.

Trong đường tròn (O), ta có $\hat{A B C} = \hat{A D C}$ (hai góc nội tiếp chắn cung AC) (2).

Từ (1) và (2) suy ra $\hat{A F E} = \hat{A D C}$ hay $\hat{A F K} = \hat{K D C}$ .

Tứ giác CDKF có góc ngoài tại đỉnh F bằng góc trong tại đỉnh D nên tứ giác CDKF nội tiếp.

Suy ra $\hat{D K F} + \hat{C K F} = 180 °$ .

Mặt khác $\hat{A C D} = 90 °$ (do AD là đường kính của (O)).

Từ đó suy ra $\hat{D K F} = 90 °$ . Suy ra $A D ⊥ E F$ tại K.

c) Tứ giác APBC nội tiếp đường tròn (O) nên $\hat{A P C} = \hat{A B C}$ . (3)

Từ (1) và (3) suy ra $\hat{A P C} = \hat{A F E}$ .

Do đó, hai tam giác APF và ACP đồng dạng (g.g).

Suy ra $\frac{A P}{A C} = \frac{A F}{A P}$ .

Nên $A P^{2} = A C . A F$ .

Lại có $A H^{2} = A C . A F$ (áp dụng hệ thức lượng trong $Δ A C H$ vuông tại H có đường cao HF).

Do đó, $A P^{2} = A H^{2}$ . Suy ra AP = AH.

Vì các tứ giác AEHF, ALHF nội tiếp nên năm điểm A, E, F, H, L cùng thuộc một đường tròn.

Suy ra tứ giác ALEF nội tiếp.

Từ đó suy ra $\hat{M E L} = \hat{L A F}$ (cùng bù với $\hat{L E F}$ ).

Lập luận tương tự với tứ giác nội tiếp ALBC, ta có $\hat{M B L} = \hat{L A C}$ .

Từ hai điều trên, suy ra $\hat{M B L} = \hat{M E L}$ .

Tứ giác MBEL có hai đỉnh kề nhau là B, E cùng nhìn cạnh ML dưới hai góc bằng nhau nên tứ giác MBEL nội tiếp.

Suy ra $\hat{M L E} = \hat{E B C}$ (cùng bù với $\hat{M B E}$ ). (4)

Từ (1) và (4) suy ra $\hat{M L E} = \hat{A F E}$ .

Lại có $\hat{A F E} + \hat{A L E} = 180 °$ (do tứ giác ALEF nội tiếp).

Do đó, $\hat{M L E} + \hat{A L E} = 180 °$ .

Vậy ba điểm A, I, M thẳng hàng.

Câu 2

Cửa hàng A niêm yết giá một bông hồng là 15 000 đồng. Nếu khách hàng mua nhiều hơn 10 bông thì từ bông thứ 11 trở đi, mỗi bông được giảm 10% trên giá niêm yết. Nếu mua nhiều hơn 20 bông thì từ bông thứ 21 trở đi, mỗi bông được giảm 20% trên giá đã giảm.

a) Nếu khách hàng mua 30 bông hồng tại cửa hàng A thì phải trả bao nhiêu tiền?

b) Bạn Thảo đã mua một số bông hồng tại cửa hàng A với số tiền là 555 000 đồng.

Hỏi bạn Thảo đã mua bao nhiêu bông hồng?

Xem đáp án

Lời giải

– Nếu mua nhiều hơn 10 bông hồng thì từ bông thứ 11 trở đi mỗi bông được giảm thêm 10% trên giá niêm yết, do đó giá mỗi bông hồng từ bông hồng thứ 11 đến 20 là:

$15 000. (100 % - 10 %) = 13 500$ (đồng).

– Nếu mua nhiều hơn 20 bông hồng thì từ bông thứ 21 trở đi mỗi bông được giảm thêm 20% trên giá đã giảm, do đó giá mỗi bông hồng từ bông hồng thứ 21 là:

$13 500. (100 % - 20 %) = 10 800$ (đồng).

a) Nếu khách hàng mua 30 bông hồng thì số tiền phải trả là:

$15 000.10 + 13 500.10 + 10 800.10 = 393 000$ (đồng).

b) Vì số tiền bạn Thảo phải trả là 555 000 > 393 000 (đồng) nên bạn đã mua nhiều hơn 30 bông hồng.

Gọi x là số bông hồng mà bạn Thảo đã mua $(x \in ℕ, x > 30)$ .

Ta có:

$15000.10 + 13500.10 + 10800 (x - 20) = 555000$

<=> x = 45 (nhận).

Vậy bạn Thảo đã mua 45 bông hồng.

Câu 3