Không sử dụng máy tính giải hệ phương trình: 2x+y=5x−3y=−1

Ta có 2x+y=5x−3y=−1⇔6x+3y=15x−3y=−1 ⇔7x=14x−3y=−1⇔x=22−3y=−1⇔x=2y=1. Vậy phương trình có nghiệm duy nhất x=2y=1

Câu hỏi:

13/07/2024 1,536

Không sử dụng máy tính giải hệ phương trình: $\{\begin{cases} 2 x + y = 5 \\ x - 3 y = - 1 \end{cases}$

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 9) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có $\{\begin{cases} 2 x + y = 5 \\ x - 3 y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} 6 x + 3 y = 15 \\ x - 3 y = - 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} 7 x = 14 \\ x - 3 y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ 2 - 3 y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = 1 \end{cases} .$

Vậy phương trình có nghiệm duy nhất

\{\begin{cases} x = 2 \\ y = 1 \end{cases}

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (O) đường kính AB. lấy điểm C thuộc (O) (C khác A và B tiếp tuyến của đường tròn (O) tại B cắt AC ở K. Từ K kẻ tiếp tuyến KD với đường tròn (O) (D là tiếp điểm khác B).

1) Chứng minh tứ giác BODK nội tiếp.

2) Biết OK cắt BD tại I. Chứng minh rằng $O I ⊥ B D$ và KC.KA = KI.KO.

3) Gọi E là trung điểm của AC, kẻ đường kính CF của đường tròn (O), FE cắt AI tại H. Chứng minh rằng H là trung điểm của AI.

Xem đáp án

Lời giải

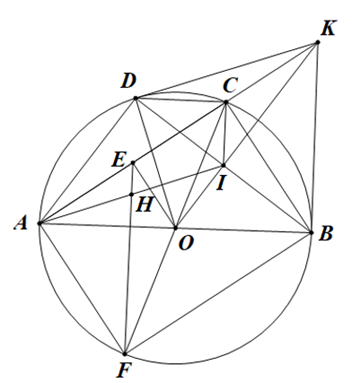
Cho đường tròn (O) đường kính AB. lấy điểm C thuộc (O) (C khác A và B tiếp tuyến của đường tròn (O) tại B cắt AC ở K. Từ K kẻ tiếp tuyến KD với đường tròn (O) (D là tiếp điểm khác B). (ảnh 1)

1) Ta có $\hat{O B K} = \hat{O D K} = 90 °$

$\Rightarrow \hat{O B K} + \hat{O D K} = 180 °$ .

Do đó tứ giác BODK nội tiếp.

2) Ta có KB = KD (tính chất hai tiếp tuyến cắt nhau).

Ta lại có OB = OD nên OK là đường trung trực của BD

Suy ra $K O ⊥ B D \Rightarrow O I ⊥ B D .$

Xét tam giác ABK vuông tại B nên $K B^{2} = K C . K A .$

Xét tam giác OBK vuông tại B nên $K B^{2} = K I \cdot K O .$

Suy ra

K C . K A = K I . K O .

(đpcm).

3) Xét KCI và KOA ta có góc K chung, $K C \cdot K A = K I \cdot K O \Leftrightarrow \frac{K C}{K I} = \frac{K O}{K A}$ .

Suy ra $Δ K C I ∽ Δ K O A (c . g . c)$ . Suy ra $\hat{K C I} = \hat{K O A}$ . (*)

Xét tam giác ACF và BAK có $\hat{K B A} = \hat{C AF} = 90 °$ (1)

Mà tam giác OAC cân tại O nên $\hat{O A C} = \hat{O C A}$ (2)

Từ (1) và (2) suy ra $Δ A C F ∽ Δ B A K$

Suy ra $\frac{B A}{B K} = \frac{A C}{AF} \Leftrightarrow \frac{2 B O}{B K} = \frac{2 A E}{AF} \Leftrightarrow \frac{B K}{AF} = \frac{B O}{A E}$ .

Xét tam giác AEF và BOK ta có $\hat{K B O} = \hat{E AF} = 90 °$ và $\frac{B K}{AF} = \frac{B O}{A E}$

Nên $Δ A E F ∽ Δ B O K$ suy ra $\hat{A E F} = \hat{B O K} \Rightarrow \hat{K EF} = \hat{K O A}$ (cùng bù với $\hat{A E F}$ ) (**)

Từ (*) và (**) ta có $\hat{K C I} = \hat{K EF}$ suy ra EF // CI.

Xét tam giác ACI có E là trung điểm của AC và EF // CI nên H là trung điểm của AI.

Câu 2

Cho phương trình x² - 2x + m - 3 = 0 (m là tham số).

a) Giải phương trình khi m = 0.

b) Tìm m để phương trình có hai nghiệm x₁ ; x₂ sao cho biểu thức $P = x_{1}^{2} + x_{2}^{2} + {(x_{1} x_{2})}^{2}$ đạt giá trị nhỏ nhất.

Xem đáp án

Lời giải

a) Khi m = 0 ta có phương trình $x^{2} - 2 x - 3 = 0$

$Δ = {(- 2)}^{2} + 12 = 16 \Rightarrow \sqrt{Δ} = 4.$

Phương trình có hai nghiệm phân biệt

$x_{1} = \frac{2 + 4}{2} = 3, x_{2} = \frac{2 - 4}{2} = - 1$ .

b) Ta có $Δ = {(- 2)}^{2} - 4 (m - 3) = - 4 m + 16$

Để phương trình có hai nghiệm thì $Δ \geq 0 \Leftrightarrow - 4 m + 16 \geq 0 \Leftrightarrow m \leq 4.$

Theo hệ thức Vi-et ta có $\{\begin{cases} x_{1} + x_{2} = 2 \\ x_{1} x_{2} = m - 3 \end{cases}$ .

Ta có $P = x_{1}^{2} + x_{2}^{2} + {(x_{1} x_{2})}^{2} = {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} + {(x_{1} x_{2})}^{2} = 2^{2} - 2 (m - 3) + {(m - 3)}^{2}$

$P = m^{2} - 8 m + 19 = {(m - 4)}^{2} + 3 \geq 3.$

Dấu “=” xảy ra khi m = 4

Vậy giá trị nhỏ nhất của P là 3 khi m = 4

Câu 3

Một mảnh vườn hình chữ nhật có diện tích 600m² . Biết rằng nếu tăng chiều dài 10m và giảm chiều rộng 5m thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng $A B = 3 cm, \hat{C} = 30 °$ .

a) Tính $\hat{B}, A C, A H$ .

b) Trên cạnh BC lấy điểm M sao cho MC = 2MB, tính diện tích tam giác AMC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho biểu thức $P = \frac{x - 9}{\sqrt{x} + 3} + \sqrt{x} + 2$ với $x \geq 0$ .

a) Rút gọn biểu thức P.

b) Tính giá trị của biểu thức P khi x = 4.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho parabol (P): y - x² và đường thẳng (d): y = x - 2.

a) Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục toạ độ Oxy.

b) Tìm toạ độ giao điểm của Parabol (P) và đường thẳng (d) bằng phép tính.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Không sử dụng máy tính giải hệ phương trình: 2x+y=5x−3y=−1

Cho phương trình x2 - 2x + m - 3 = 0 (m là tham số). a) Giải phương trình khi m = 0. b) Tìm m để phương trình có hai nghiệm x1 ; x2 sao cho biểu thức P=x12+x22+x1x22 đạt giá trị nhỏ nhất.

Một mảnh vườn hình chữ nhật có diện tích 600m2 . Biết rằng nếu tăng chiều dài 10m và giảm chiều rộng 5m thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.

Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng AB=3 cm, C^=30°. a) Tính B^, AC, AH. b) Trên cạnh BC lấy điểm M sao cho MC = 2MB, tính diện tích tam giác AMC.

Cho biểu thức P=x−9x+3+x+2 với x≥0. a) Rút gọn biểu thức P. b) Tính giá trị của biểu thức P khi x = 4.

Cho parabol (P): y - x2 và đường thẳng (d): y = x - 2. a) Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục toạ độ Oxy. b) Tìm toạ độ giao điểm của Parabol (P) và đường thẳng (d) bằng phép tính.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Không sử dụng máy tính giải hệ phương trình: $\{\begin{cases} 2 x + y = 5 \\ x - 3 y = - 1 \end{cases}$

Cho phương trình x² - 2x + m - 3 = 0 (m là tham số).

a) Giải phương trình khi m = 0.

b) Tìm m để phương trình có hai nghiệm x₁ ; x₂ sao cho biểu thức $P = x_{1}^{2} + x_{2}^{2} + {(x_{1} x_{2})}^{2}$ đạt giá trị nhỏ nhất.

Một mảnh vườn hình chữ nhật có diện tích 600m² . Biết rằng nếu tăng chiều dài 10m và giảm chiều rộng 5m thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.

Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng $A B = 3 cm, \hat{C} = 30 °$ .

a) Tính $\hat{B}, A C, A H$ .

b) Trên cạnh BC lấy điểm M sao cho MC = 2MB, tính diện tích tam giác AMC.

Cho biểu thức $P = \frac{x - 9}{\sqrt{x} + 3} + \sqrt{x} + 2$ với $x \geq 0$ .

a) Rút gọn biểu thức P.

b) Tính giá trị của biểu thức P khi x = 4.

Cho parabol (P): y - x² và đường thẳng (d): y = x - 2.

a) Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục toạ độ Oxy.

b) Tìm toạ độ giao điểm của Parabol (P) và đường thẳng (d) bằng phép tính.