Câu hỏi:
13/07/2024 15,634
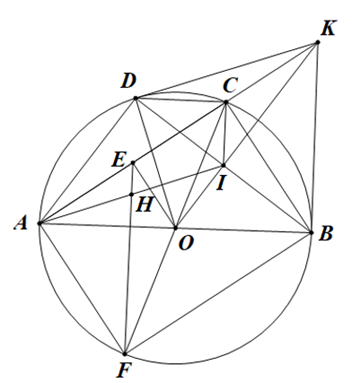
Cho đường tròn (O) đường kính AB. lấy điểm C thuộc (O) (C khác A và B tiếp tuyến của đường tròn (O) tại B cắt AC ở K. Từ K kẻ tiếp tuyến KD với đường tròn (O) (D là tiếp điểm khác B).
1) Chứng minh tứ giác BODK nội tiếp.
2) Biết OK cắt BD tại I. Chứng minh rằng và KC.KA = KI.KO.
3) Gọi E là trung điểm của AC, kẻ đường kính CF của đường tròn (O), FE cắt AI tại H. Chứng minh rằng H là trung điểm của AI.
Cho đường tròn (O) đường kính AB. lấy điểm C thuộc (O) (C khác A và B tiếp tuyến của đường tròn (O) tại B cắt AC ở K. Từ K kẻ tiếp tuyến KD với đường tròn (O) (D là tiếp điểm khác B).
1) Chứng minh tứ giác BODK nội tiếp.
2) Biết OK cắt BD tại I. Chứng minh rằng và KC.KA = KI.KO.
3) Gọi E là trung điểm của AC, kẻ đường kính CF của đường tròn (O), FE cắt AI tại H. Chứng minh rằng H là trung điểm của AI.
Câu hỏi trong đề:
Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 9) !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Ta có
.
Do đó tứ giác BODK nội tiếp.
2) Ta có KB = KD (tính chất hai tiếp tuyến cắt nhau).
Ta lại có OB = OD nên OK là đường trung trực của BD
Suy ra
Xét tam giác ABK vuông tại B nên
Xét tam giác OBK vuông tại B nên
Suy ra (đpcm).3) Xét KCI và KOA ta có góc K chung, .
Suy ra . Suy ra . (*)
Xét tam giác ACF và BAK có (1)
Mà tam giác OAC cân tại O nên (2)
Từ (1) và (2) suy ra
Suy ra .
Xét tam giác AEF và BOK ta có và
Nên suy ra (cùng bù với ) (**)
Từ (*) và (**) ta có suy ra EF // CI.
Xét tam giác ACI có E là trung điểm của AC và EF // CI nên H là trung điểm của AI.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho phương trình x2 - 2x + m - 3 = 0 (m là tham số).
a) Giải phương trình khi m = 0.
b) Tìm m để phương trình có hai nghiệm x1 ; x2 sao cho biểu thức đạt giá trị nhỏ nhất.
Cho phương trình x2 - 2x + m - 3 = 0 (m là tham số).
a) Giải phương trình khi m = 0.
b) Tìm m để phương trình có hai nghiệm x1 ; x2 sao cho biểu thức đạt giá trị nhỏ nhất.
Xem đáp án »
13/07/2024
10,182
Câu 2:
Một mảnh vườn hình chữ nhật có diện tích 600m2 . Biết rằng nếu tăng chiều dài 10m và giảm chiều rộng 5m thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
Một mảnh vườn hình chữ nhật có diện tích 600m2 . Biết rằng nếu tăng chiều dài 10m và giảm chiều rộng 5m thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
Xem đáp án »
13/07/2024
7,611
Câu 3:
Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng .
a) Tính .
b) Trên cạnh BC lấy điểm M sao cho MC = 2MB, tính diện tích tam giác AMC.
Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng .
a) Tính .
b) Trên cạnh BC lấy điểm M sao cho MC = 2MB, tính diện tích tam giác AMC.
Xem đáp án »
13/07/2024
6,085
Câu 4:
Cho biểu thức với .
a) Rút gọn biểu thức P.
b) Tính giá trị của biểu thức P khi x = 4.
Cho biểu thức với .
a) Rút gọn biểu thức P.
b) Tính giá trị của biểu thức P khi x = 4.
Xem đáp án »
13/07/2024
3,184
Câu 5:
Cho parabol (P): y - x2 và đường thẳng (d): y = x - 2.
a) Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục toạ độ Oxy.
b) Tìm toạ độ giao điểm của Parabol (P) và đường thẳng (d) bằng phép tính.
Cho parabol (P): y - x2 và đường thẳng (d): y = x - 2.
a) Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục toạ độ Oxy.
b) Tìm toạ độ giao điểm của Parabol (P) và đường thẳng (d) bằng phép tính.
Xem đáp án »
13/07/2024
1,088
về câu hỏi!