Câu hỏi trong đề: Giải SGK Toán 12 Cánh diều Bài tập cuối Chương I có đáp án !!
Quảng cáo
Trả lời:
b) y = – x3 + 3x2 – 6x
1) Tập xác định: ℝ.
2) Sự biến thiên:
Giới hạn tại vô cực: .
y' = – 3x2 + 6x – 6 = – 3(x2 – 2x + 1) – 3 = – 3(x – 1)2 – 3 < 0 với mọi x ∈ ℝ;
Bảng biến thiên:
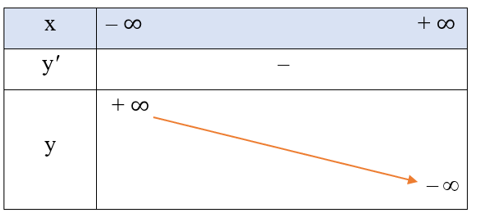
Hàm số nghịch biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
Đồ thị hàm số đi qua gốc tọa độ O(0; 0).
Đồ thị hàm số đi qua các điểm (0; 0), (1; – 4), (2; – 8).
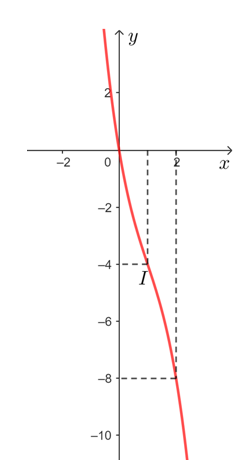
Vậy đồ thị hàm số y = – x3 + 3x2 – 6x được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là gốc tọa độ I(1; – 4).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
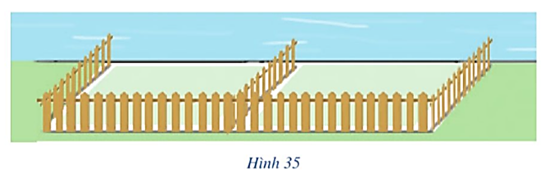
Giả sử chiều dài từng mặt của ba mặt hàng rào song song nhau là x (m).
Chi phí để làm ba mặt hàng rào song song là: 3 ∙ x ∙ 50 000 = 150 000x (đồng).
Chi phí để làm mặt hàng rào song song với bờ sông là: 15 000 000 – 150 000x (đồng).
Chiều dài của mặt hàng rào song song với bờ sông là
(m).
Rõ ràng, x phải thỏa mãn điều kiện 0 < x < 100.
Giả sử diện tích hàng rào không đáng kể, khi đó diện tích hai khu đất thu được sau khi làm hàng rào là S(x) = (m2).
Xét hàm số với x ∈ (0; 100).
Ta có S'(x) = .
Trên khoảng (0; 100), S'(x) = 0 khi x = 50.
Bảng biến thiên của hàm số S(x) như sau:
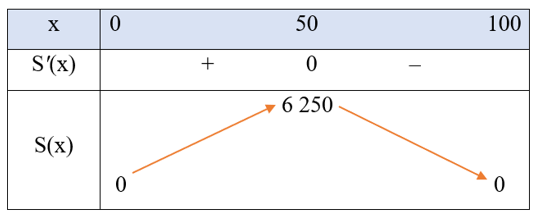
Căn cứ bảng biến thiên, ta thấy: Trên khoảng (0; 100), hàm số S(x) đạt giá trị lớn nhất bằng 6 250 tại x = 50.
Vậy diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào là 6 250 m2.
Lời giải
Gọi x (cm) là chiều rộng của trang sách.
Khi đó, chiều dài của trang sách là (cm).
Sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là x – 4 (cm) và chiều dài là (cm).
Rõ ràng, x phải thỏa mãn điều kiện 4 < x < 64.
Diện tích phần in chữ trên trang sách là
S(x) = (cm2).
Xét hàm số S(x) = với x ∈ (4; 64).
Ta có S'(x) = < 0;
S'(x) = 0 ⇔ – 6x2 + 1 536 = 0 ⇔ x = – 16 hoặc x = 16.
Khi đó trên khoảng (4; 64), S'(x) = 0 khi x = 16.
Bảng biến thiên của hàm số S(x) như sau:
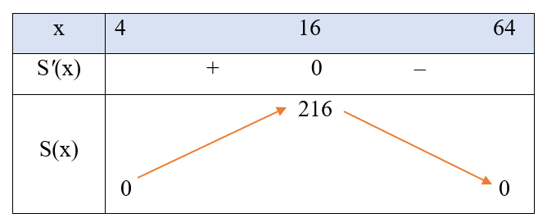
Căn cứ vào bảng biến thiên, ta thấy: Trên khoảng (4; 64), hàm số S(x) đạt giá trị lớn nhất bằng 216 tại x = 16. Khi đó, .
Vậy kích thước tối ưu của trang sách là 16 × 24 (cm) thì in chữ trên trang sách có diện tích lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.