Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB.
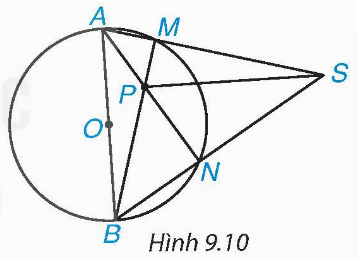
Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB.
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài 27. Góc nội tiếp có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét đường tròn (O) có: 
và 
đều là góc nội tiếp cùng chắn nửa đường tròn nên 
và 
Suy ra BM ⊥ AM và AN ⊥ BN
Hay BM ⊥ AS và AN ⊥ BS.
Xét ∆ABS có AN, BM là hai đường cao (BM ⊥ AS và AN ⊥ BS) cắt nhau tại P nên P là trực tâm của ∆ABS, suy ra SP ⊥ AB.
Vậy SP ⊥ AB.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
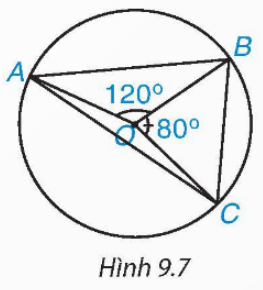
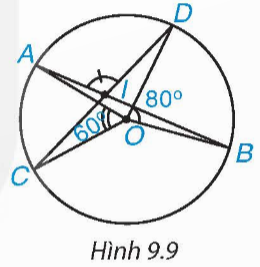
Xét đường tròn (O) có 
là hai góc nội tiếp cùng chắn cung nhỏ AB nên
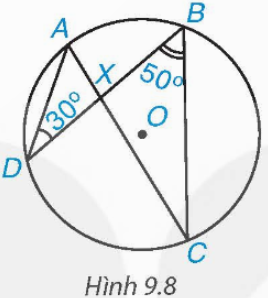
Vì 
là góc ngoài của ∆BXC tại đỉnh X nên ta có:
Vậy 
Lời giải
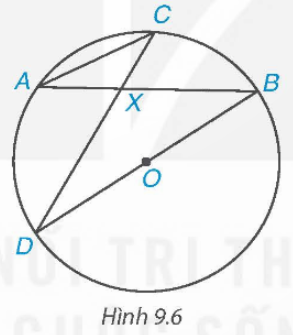
Xét đường tròn tâm O, có 
và 
là hai góc nội tiếp cùng chắn cung nhỏ AD
Suy ra 
hay 
Xét ∆AXC và ∆DXB có:
(hai góc đối đỉnh) và 
(chứng minh trên)
Do đó ∆AXC ᔕ ∆DXB (g.g).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập