Câu hỏi:
13/07/2024 155
Đà Lạt là thành phố du lịch, có khí hậu mát mẻ. Nơi đây trồng nhiều loại hoa để phục vụ nhu cầu trong nước và xuất khẩu. Giả sử người ta trồng hoa trên một mảnh vườn có dạng hình chữ nhật với diện tích là 240 m2, chu vi là 68 m.
Làm thế nào để xác định được chiều dài, chiều rộng của mảnh vườn trồng hoa nói trên?
Đà Lạt là thành phố du lịch, có khí hậu mát mẻ. Nơi đây trồng nhiều loại hoa để phục vụ nhu cầu trong nước và xuất khẩu. Giả sử người ta trồng hoa trên một mảnh vườn có dạng hình chữ nhật với diện tích là 240 m2, chu vi là 68 m.
Làm thế nào để xác định được chiều dài, chiều rộng của mảnh vườn trồng hoa nói trên?
Câu hỏi trong đề: Giải SGK Toán 9 CD Bài 3. Định lí Viète có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi hai kích thước của mảnh vườn hình chữ nhật là x1; x2 (m) (x1 > 0, x2 > 0).
Ta có nửa chu vi và diện tích mảnh vườn hình chữ nhật lần lượt là x1 + x2 (m) và x1x2 (m2).
Theo bài, mảnh vườn dạng hình chữ nhật có chu vi là 68 m nên nửa chu vi của mảnh vườn là 68 : 2 = 34 (m), do đó x1 + x2 = 34.
Diện tích mảnh vườn hình chữ nhật là 240 m2, do đó x1x2 = 240.
Khi đó, x1 và x2 là hai nghiệm của phương trình: x2 – 34x + 240 = 0.
Phương trình trên có các hệ số a = 1, b = –34, c = 240.
Do b = –34 nên b’ = –17.
Ta có: ∆’ = (–17)2 – 1.240 = 49 > 0.
Do ∆’ > 0 nên phương trình có hai nghiệm phân biệt là:
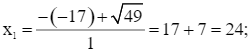
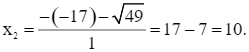
Cả hai giá trị trên đều thỏa mãn điều kiện lớn hơn 0.
Vậy chiều dài và chiều rộng của mảnh vườn đó lần lượt là 24 (m) và 10 (m) (do chiều dài luôn lớn hơn chiều rộng).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: 
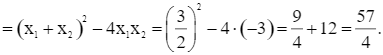
Mà 
nên ta có:
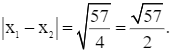
Lời giải
Xét phương trình ax2 + bx + c (a ≠ 0) có ac < 0, theo kết quả của Bài 2, trang 59, SGK Toán lớp 9, Tập 2 thì phương trình trên luôn có hai nghiệm phân biệt.
Khi đó, theo định lí Viète, ta có: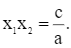 
Mà ac < 0 nên a và c là hai số trái dấu.
Lại có a ≠ 0 nên ta suy ra được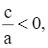 
hay x1x2 < 0.
Do đó x1, x2 là hai số trái dấu nhau.
Vậy nếu ac < 0 thì phương trình ax2 + bx + c (a ≠ 0) có hai nghiệm là hai số trái dấu nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận