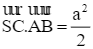Phát biểu nào sau đây là đúng?
A. Với hai vectơ bất kì 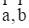 và số thực k, ta có: k(
và số thực k, ta có: k(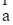 +
+ 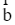 ) = k
) = k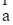 + k
+ k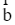 .
.
B. Với hai vectơ bất kì 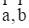 và số thực k, ta có: k(
và số thực k, ta có: k(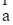 +
+ 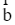 ) =
) = 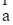 k +
k + 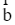 k.
k.
C. Với hai vectơ bất kì 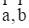 và số thực k, ta có: (
và số thực k, ta có: (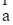 +
+ 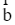 )k =
)k = 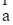 k +
k + 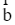 k.
k.
D. Với hai vectơ bất kì 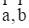 và số thực k, ta có: k(
và số thực k, ta có: k(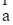 +
+ 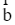 ) = k
) = k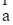 +
+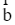 k.
k.
Phát biểu nào sau đây là đúng?
A. Với hai vectơ bất kì ![]() và số thực k, ta có: k(
và số thực k, ta có: k(![]() +
+ ![]() ) = k
) = k![]() + k
+ k![]() .
.
B. Với hai vectơ bất kì ![]() và số thực k, ta có: k(
và số thực k, ta có: k(![]() +
+ ![]() ) =
) = ![]() k +
k + ![]() k.
k.
C. Với hai vectơ bất kì ![]() và số thực k, ta có: (
và số thực k, ta có: (![]() +
+ ![]() )k =
)k = ![]() k +
k + ![]() k.
k.
D. Với hai vectơ bất kì ![]() và số thực k, ta có: k(
và số thực k, ta có: k(![]() +
+ ![]() ) = k
) = k![]() +
+![]() k.
k.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Với hai vectơ bất kì ![]() và số thực k, ta có: k(
và số thực k, ta có: k(![]() +
+ ![]() ) = k
) = k![]() + k
+ k![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
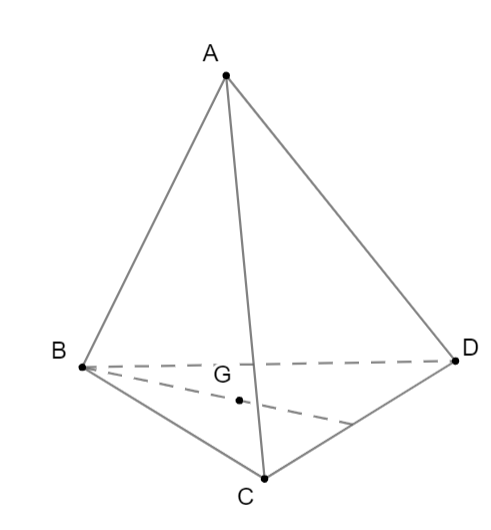
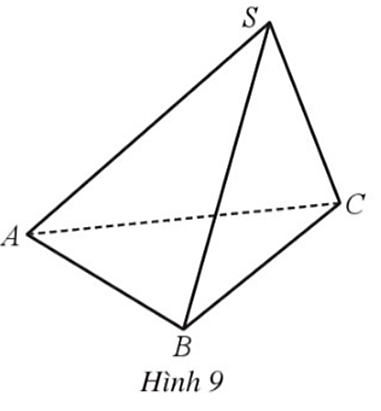
Do G là trọng tâm tam giác BCD nên ![]() . Vậy đáp án A đúng.
. Vậy đáp án A đúng.
Do G là trọng tâm tam giác BCD, có ![]() nên ta có:
nên ta có:
![]() . Vậy đáp án B sai.
. Vậy đáp án B sai.
Có ![]() =
= ![]() =
= ![]() =
= ![]() . Vậy đáp án C đúng.
. Vậy đáp án C đúng.
Có ![]()
![]()
= ![]() .
.
Vậy đáp án D đúng.
Lời giải
|
a) Đ |
b) Đ |
c) S |
d) Đ |
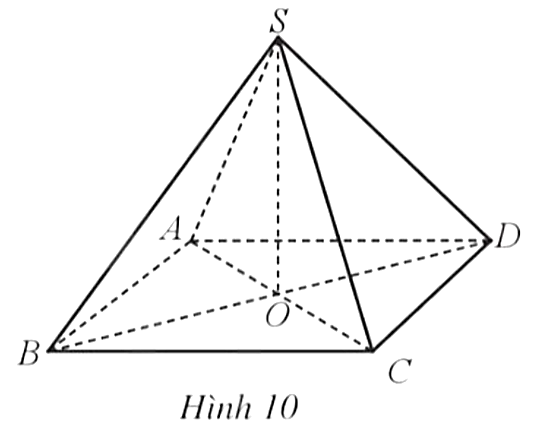
Theo đề bài, hình chóp tứ giác có tất cả các cạnh bằng a nên S.ABCD là hình chóp tứ giác đều do đó đáy ABCD là hình vuông.
Đáy ABCD là hình vuông cạnh a nên độ dài đường chéo AC = BD = ![]() .
.
Tam giác SAC có SA = SC = a, AC = ![]() .
.
Áp dụng định lý Pythagore đảo có SA2 + SC2 = AC2 do đó tam giác SAC vuông cân tại S, suy ra ![]() = 45°.
= 45°.
Do đó, ![]() = 180° −
= 180° − ![]() = 180° − 45° = 135°.
= 180° − 45° = 135°.
![]() =
= ![]() = a.
= a.![]() .
.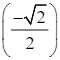 = −a2.
= −a2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.