Chọn phương án đúng.

Cho hình chữ nhật ABCD có AB = 3 cm, BC = 4 cm và nội tiếp đường tròn (O; R). Khẳng định nào sau đây là sai?

A. O là trung điểm của AC.

B. O là trung điểm của BD.

C. R = 5 cm.

D. R = 2,5 cm.

Xem lời giải

Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài 29. Tứ giác nội tiếp có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: C

Chọn phương án đúng. Cho hình chữ nhật ABCD có AB = 3 cm, BC = 4 cm và nội tiếp đường tròn (O; R). Khẳng định nào sau đây là sai? A. O là trung điểm của AC. B. O là trung điểm của BD. C. R = 5 cm. D. R = 2,5 cm. (ảnh 1)

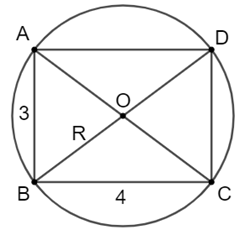
Tâm đường tròn ngoại tiếp của hình chữ nhật là giao điểm của hai đường chéo.

Suy ra điểm O là giao điểm của AC và BD, hay O là trung điểm mỗi đường.

Bán kính đường tròn ngoại tiếp của hình chữ nhật bằng một nửa độ dài đường chéo suy ra \(R = \frac{{AC}}{2}.\)

Theo định lí Pythagore, ta có: AC² = AB² + BC² hay \(AC = \sqrt {{3^2} + {4^2}} = 5\) (cm).

Do đó \(R = \frac{5}{2} = 2,5\) cm.

Vậy khẳng định C là khẳng định sai.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Người ta muốn dựng một khung cổng hình chữ nhật rộng 4 m và cao 3 m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như hình bên. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó.

Xem đáp án

Lời giải

Người ta muốn dựng một khung cổng hình chữ nhật rộng 4 m và cao 3 m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như hình bên. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó. (ảnh 2)

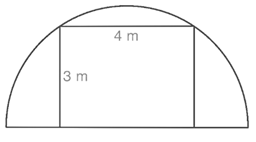
Khung cổng là một nửa của hình chữ nhật với kích thước 6 m × 4 m và nội tiếp một đường tròn với một nửa là khung thép trên.

Đường chéo của hình chữ nhật với kích thước 6 m × 4 m là \(\sqrt {{6^2} + {4^2}} = 2\sqrt {13} \) (m).

Vậy bán kính đường tròn đó là \(R = \frac{{2\sqrt {13} }}{2} = \sqrt {13} \) (m).

Chiều dài đoạn thép để làm khung nửa đường tròn bằng với độ dài của nửa đường tròn trên và bằng \(\frac{{2\sqrt {13} \pi }}{2} = \sqrt {13} \pi \approx 11,32\) (m).

Câu 2

Cho ABCD là tứ giác nội tiếp. Tính số đo các góc còn lại của tứ giác trong mỗi trường hợp sau:

a) \[\widehat A = 60^\circ ,\] \[\widehat B = 80^\circ .\]

b) \[\widehat B = 70^\circ ,\] \[\widehat C = 90^\circ .\]

c) \[\widehat C = 100^\circ ,\] \[\widehat D = 60^\circ .\]

d) \[\widehat D = 110^\circ ,\] \[\widehat A = 80^\circ .\]

Xem đáp án

Lời giải

a) \[\widehat C = 180^\circ - \widehat A = 180^\circ - 60^\circ = 120^\circ ,\]

\[\widehat D = 180^\circ - \widehat B = 180^\circ - 80^\circ = 100^\circ ;\]

b) \[\widehat A = 180^\circ - \widehat C = 180^\circ - 90^\circ = 90^\circ ,\]

\[\widehat D = 180^\circ - \widehat B = 180^\circ - 70^\circ = 110^\circ ;\]

c) \[\widehat A = 180^\circ - \widehat C = 180^\circ - 100^\circ = 80^\circ ,\]

\[\widehat B = 180^\circ - \widehat D = 180^\circ - 60^\circ = 120^\circ ;\]

d) \[\widehat C = 180^\circ - \widehat A = 180^\circ - 80^\circ = 100^\circ ,\]

\[\widehat B = 180^\circ - \widehat D = 180^\circ - 110^\circ = 70^\circ .\]

Câu 3