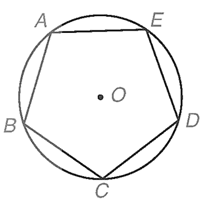
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một bát giác đều hay không? Vì sao?
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một bát giác đều hay không? Vì sao?
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung trang 90 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
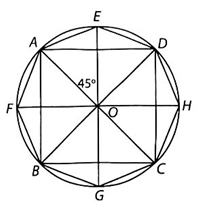
a) Các điểm E, F, G, H cùng nằm trên đường tròn (O) và được vẽ như hình bên.
b) Do \(\widehat {AOE} = \widehat {BOF} = \widehat {COG} = \widehat {DOH} = 45^\circ \) nên \[\widehat {EOD} = \widehat {FOA} = \widehat {GOB} = \widehat {HOC} = 45^\circ \] (vì các góc AOD, BOA, COB, DOC vuông cân tại O).
Do vậy các tam giác AOE, BOF, COG, DOH, EOD, FOA, GOB, HOC bằng nhau theo trường hợp cạnh – góc − cạnh.
Suy ra EA = AF = FB = BG = GC = CH = HD = DE.
Vậy bát giác EAFBGCHD lồi có các cạnh bằng nhau và nội tiếp đường tròn (O).
Hơn nữa các đỉnh của bát giác chia đường tròn thành 8 cung nhỏ với số đo mỗi cung là 45°.
Do vậy các góc của bát giác lồi là các góc nội tiếp chắn đúng 6 cung nhỏ trên nên chúng bằng nhau và có số đo bằng \(\frac{6}{8}.360^\circ = 270^\circ .\)
Vậy EAFBGCHD là bát giác đều.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
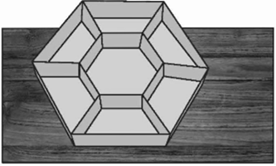
Nếu chia đôi lục giác đều nhỏ bởi một đường kính thì ta sẽ được hai hình thang cân nhỏ bằng nhau và bằng với các hình thang cân trước đó.
Do vậy đường kính của lục giác đều nhỏ phải bằng cạnh của lục giác đều lớn, tức là bằng 10 cm.
Vì vậy, cạnh của lục giác đều nhỏ bằng \(\frac{1}{2}.10 = 5\) (cm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
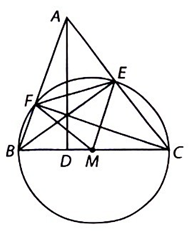
Lấy M là trung điểm của BC. Do BCE, BCF là các tam giác vuông có chung cạnh huyền BC nên ME = MB = MC = MF. Do đó đường tròn (M, MB) ngoại tiếp tứ giác BCEF.
Tương tự, CAFD và ABDE cũng là các tứ giác nội tiếp.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập