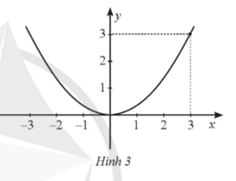
Cho A là giao điểm của hai đường thẳng y = x – 1 và y = –2x + 8. Chứng minh rằng điểm A thuộc đồ thị hàm số \(y = \frac{2}{9}{x^2}.\)
Cho A là giao điểm của hai đường thẳng y = x – 1 và y = –2x + 8. Chứng minh rằng điểm A thuộc đồ thị hàm số \(y = \frac{2}{9}{x^2}.\)
Quảng cáo
Trả lời:
Gọi A(x0; y0) là giao điểm của hai đường thẳng y = x – 1 và y = –2x + 8.
Do đó ta có:
⦁ y0 = x0 – 1;
⦁ y0 = –2x0 + 8.
Suy ra: x0 – 1 = –2x0 + 8.
3x0 = 9
x0 = 3.
Thay x0 = 3 vào hàm số \(y = \frac{2}{9}{x^2},\) ta được: \({y_0} = \frac{2}{9} \cdot {3^2} = 2.\)
Suy ra A(3; 2).
Mặt khác, thay x0 = 3 và y0 = 2 vào hàm số \(y = \frac{2}{9}{x^2},\) ta có \(2 = \frac{2}{9} \cdot {3^2}\) (luôn đúng), nên điểm A thuộc đồ thị hàm số \(y = \frac{2}{9}{x^2}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
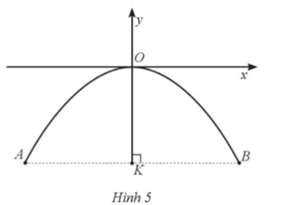
Từ Hình 5, ta có K(0; –4,5).
Gọi hoành độ của điểm B là b (b > 0).
Do tung độ của điểm B bằng tung độ của K nên B(b; –4,5).
Mặt khác, B thuộc parabol \(y = - \frac{1}{8}{x^2}\) nên ta có:
\( - 4,5 = - \frac{1}{8}{b^2}\) hay b2 = 36, nên b = 6 (do b > 0).
Từ đó KB = 6 m và AB = 2.KB = 2.6 = 12 m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất bằng 12 mét.
Lời giải
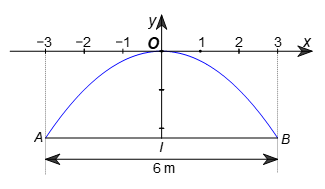
Gọi I là trung điểm của đoạn AB. Khi đó OI = h và \(AI = IB = \frac{{AB}}{2} = \frac{6}{2} = 3\,\,\left( {\rm{m}} \right).\)
Từ đó, trong hệ trục Oxy, hoành độ của B bằng 3, tung độ của B bằng –h.
Do đó: \( - h = - \frac{1}{4} \cdot {3^2}\) hay \( - h = \frac{{ - 9}}{4},\) suy ra \(h = \frac{9}{4} = 2,25\,\,\left( {\rm{m}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.